Одно: n = 9376
Объяснение:
n(n-1) делится на 10^4.
Если одно из чисел (n или n-1) не делится ни на 2, ни на 5, то оно взаимно просто с 10000, и другое число обязано делиться на 10000. Очевидно, таких четырехзначных n, что n или n-1 делится на 10000, нет. Значит, оба числа делятся на 2 или на 5. Два числа вместе делиться на 2 или на 5 не могут, т.к. различаются на 1. Значит, одно из них делится на 2 (не делится на 5), а другое на 5 (не делится на 2).
Пусть, n =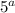 
* b (a - степень вхождения 5 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 5, поэтому, чтобы n(n-1) делилось на 
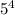, нужно чтобы а было ≥ 4.
n ≡ 0 mod .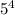
Аналогично n-1 ≡ 0 mod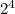 
(т.к. n не делится на 2) ⇒ n ≡ 1 mod 2^4
Видно, что n = 625 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы 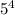* 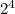= 10000, умноженной на целое число. Значит, таких четырехзначных n не существует.
Пусть, n =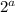 
* b (a - степень вхождения 2 в разложение n, a≥1). Т.к. n-1 и n взаимно просты, n-1 не делится на 2, поэтому, чтобы n(n-1) делилось на 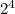, нужно чтобы а было ≥ 4.
n ≡ 0 mod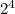
Аналогично n-1 ≡ 0 mod 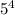(т.к. n не делится на 5) ⇒ n ≡ 1 mod 5^4
Видно, что n = 9376 подходит. По кит. т. об остатках, все остальные n получаются прибавлением константы 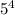* 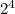= 10000, умноженной на целое число. Значит, существует только 1 четырехзначное n = 9376.
Если моё решение Вам отметьте его как лучшее.
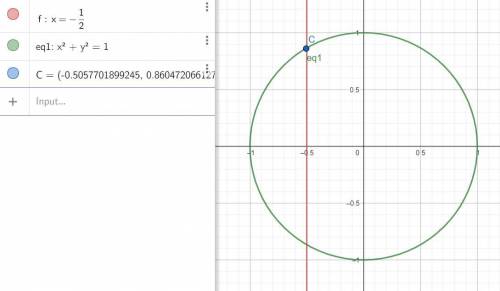
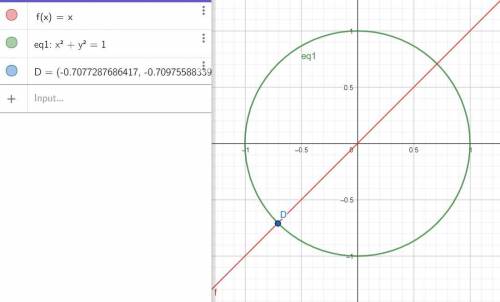
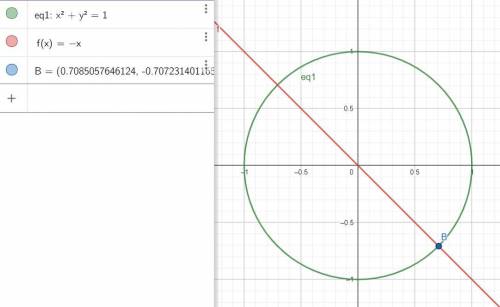
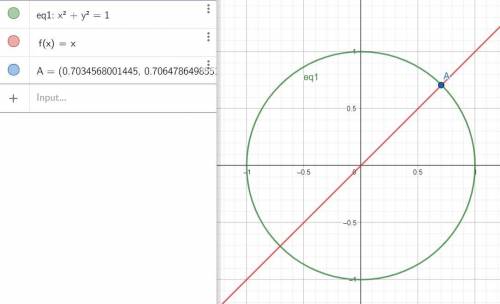
см. рисунок
1) А
2) В
3) С
4) D
Объяснение:
а) 2пи - полный оборот, поэтому все точки будут слиты в одну. 6 пи, 8 пи кратны 2 пи поэтому там то же самое. вывод: достаточно построить 1 точку в каждом случае
б) пи на четыре = 45 градусов. табличное значение.
в) пи на три = 60 градусов. табличное значение
г) при единичном круге х = косинус угла поворота у = синус угла поворота
д) реально строить хорошо - прочертить круг и пересекать его лучом соответствующего угла отклонения. Для 1) и 2) и 4)
Для 3) 2 пи на три = 120 градусов, т.е. 90 + 30, у єтих точек абсциса (х) будет = 1/2 по табличному значению синуса - посему - линия по этой абсцисе - и точка пересечения с кругом - искомая.
потянет на лучший ответ?
Разумеется, имеют смысл при соблюдении ОДЗ логарифма:
a > 0, a ≠ 1, x > 0.
Для этой записи
имеет смысл (ОДЗ логарифма0:
x > 0, x ≠ 1, a > 0.