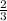от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
Поясняю:
у=х*2 + 1 - это парабола, ветви которой направлены вверх и смещенная по оси у на 1 единицу вверх; х=1 - это прямая, параллельная оси у и проходящая через точку (1;0); х=4 - это прямая, проходящая черезточку (4;0); у=0 - это прямая, параллельная оси х, проходящая через точку (0;0), точнее это ось х и есть.
Жаль нарисовать не могу, попытаюсь описать словами:
значит, проводим оси х и у; строим параболу(ее вершина будет в точке(0;1), ветви идут вверх, остальные точки не имеют значения, проводит параболу произвольно, здесь главное вершина); строим прямую х=1(т.е. через точку (1;0) проводим прямую, параллельную оси у; строим прямую х=4(через точку(4;0) проводим прямую, параллельную оси у); строим прямую у=0 - это ось х и есть; на чертеже находим фигуру, которая образована всеми 3-мя графиками прямых и графиком параболы; после этого находим ее границы по оси х( в нашем случае фигура лежит в пределах от 1 до 4); теперь берем интеграл от той ф-ции, которая даст нам площадь фигуры, а по геометрическому определению интеграл - это площадь фигуры, лежащей под графиком ф-ции; в нашем случае, такой ф-цией является уравнение параболы. Значит берем нтеграл от выражения у=х*2 + 1 в пределах от 1 до 4(т.е нижней границей интегрирования является1, а верхней-4)
В итоге получим, что площадь равна 24 кв.ед.
Ниже прилагаю рисунок