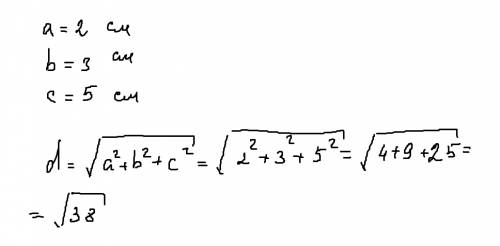
1). R = 12 см
l = 2πR·α / 360°
1. l = 2π·12·36° / 360° = 24π/10 = 2,4π см
2. l = 2π·12·72° / 360° = 4,8π см
3. l = 2π·12·45° / 360° = 3π см
4. l = 2π·12·15° / 360° = π см
2) l = 2πR R = l / (2π)
S = πR² = πl² / (4π²) = l² / (4π)
1. l = 6π см
S = 36π² / (4π) = 9π см
2. l = 4π см
S = 16π² / (4π) = 4π см²
3. l = 10π см
S = 100π² / (4π) = 25π см²
4. l = 8π см
S = 64π² / (4π) = 16π см²
3)
а) R = 12 см,
l = πR·α / 180°
α = l · 180° / (πR)
1. l = 2π см
α = 2π · 180° / (12π) = 30°
2. l = 3π см
α = 3π · 180° / (12π) = 45°
б) R = 10 см,
Sсект = πR²·α / 360°
α = Sсект·360° / (πR²)
1. Sсект = 5π см²
α = 5π·360° / (100π) = 18°
2. Sсект = 10π см²
α = 10π·360° / (100π) = 36°
6 (км/час) - скорость первого туриста.
5 (км/час) - скорость второго туриста.
Объяснение:
Из пунктов А и В, расстояние между которыми 33 км, выходят одновременно два туриста и встречаются через 3 часа.
Найти скорость каждого туриста, если турист, вышедший из пункта А на 3 км больше.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х – скорость первого туриста.
у - скорость второго туриста.
3*х – расстояние первого туриста.
3*у – расстояние второго туриста.
Составить систему уравнений согласно условию задачи:
3х+3у=33
3х-3у=3
Разделить оба уравнения на 3 для упрощения:
х+у=11
х-у=1
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=11-у
11-у-у=1
-2у=1-11
-2у= -10
у= -10/-2
у=5 (км/час) - скорость второго туриста.
х=11-у
х=11-5
х=6 (км/час) - скорость первого туриста.
Проверка:
6*3+5*3=18+15=33;
6*3-5*3=18-15=3, верно.