#1. у=х ^2.
Подставить координаты точки в уравнение. Если получится верное равенство, то точка принадлежит графику функции, если нет - не принадлежит.
а) А( 6; 36) : 36=6^2
36=36 ответ:принадлежит
б) В(-1,5; 2,25): 2,25=(-1,5)^2
2,25=2,25 ответ:принадлежит
в) С( 4; -2): -2=4^2
-2<>16 ответ: не принадлежит
г) Д(1,2; 1,44): 1,44=1,2^2
1,44=1,44 ответ:принадлежит
# 2. При каких значениях а точка Р( а; 64) принадлежит графику функции
а) у=х ^2. 64=x^2
x1=8, x2=-8 ответ: Р( 8; 64) и Р( -8; 64)
б) у= х^3. 64=x^3
x=4 ответ: Р( 4; 64)
1. записываем пример.
2. раскрываем формулу разности квадратов (x^2-y^2) и закрываем формулу квадрата разности (x^2-2xy+y^2) и одновременно с этим проводим другие действия. при раскрытии формулы разности квадратов получается (x-y)(x+y). при закрытии формулы квадрата разности получается (x-y)^2. значит, это можно раскрыть как выражение (x-y), возведенное в квадрат, то есть, умножить это выражение на такое же. получается (x-y)(x-y). проводим остальные действия: выносим общие множители выражений за скобки и превращаем вторую дробь в обратную. в итоге получаются сократимые выражения, состоящие из множителей. (x+2y) сокращается в числителе первой дроби и в знаменателе второй. (x-y) сокращается в знаменателе первой дроби и в числителе второй. далее просто умножаем оставшиеся выражения на множители, которые выносили ранее. ответ:
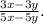
вывод. применение формул сокращенного умножения - их нужно закрывать или раскрывать в зависимости от того, что требуется в примере.
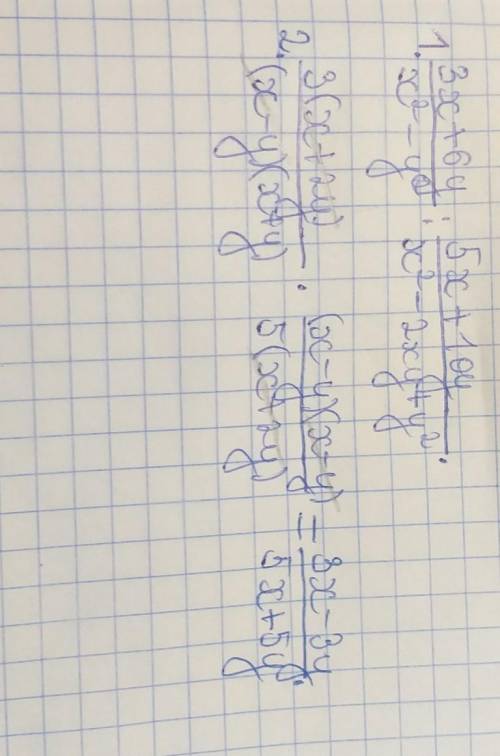
6* (-1) = q = -6
y = x^2 +px +q = x^2 -5x -6