Два отдела института купили бумагу и скрепки.один отдел за 5 пачек бумаги и 4 коробки скрепок заплатили 114р., а второй отдел за 2 коробки скрепок заплатили 60р . сколько стоит одна пачка бумаги и одна коробка скрепок

👇

Ответ:

semak03

07.06.2021

х - стоит одна пачка бумаги
у - Сколько стоит одна коробка скрепок

5х+3у=114
2у=60

у=60:2=30

5х+3у=114
5х+3*30=114
5х=114-90
5х=24
х=4.8
ответ : одна пачка бумаги стоит 4.8р.,одна коробка скрепокстоит одна 30р.

4,4(90 оценок)

Открыть все ответы

Ответ:

Mabmbj

07.06.2021

рассмотрим наше уравнение:

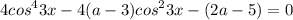
$\displaystyle 4cos^43x-4(a-3)cos^23x-(2a-5)=0$

выполним замену cos²3x=t; t≥0

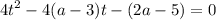
$\displaystyle 4t^2-4(a-3)t-(2a-5)=0$

чтобы уравнение имело хотя бы один корень надо чтобы D≥0

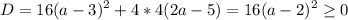
$\displaystyle D=16(a-3)^2+4*4(2a-5)=16(a-2)^2\geq 0$

Это неравенство выполняется для любых a

тогда проверим корни, необходимо чтобы t≥0

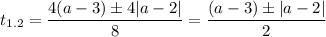
$\displaystyle t_{1.2}=\frac{4(a-3)\pm 4|a-2|}{8}=\frac{(a-3)\pm |a-2|}{2}$

рассмотрим первый корень

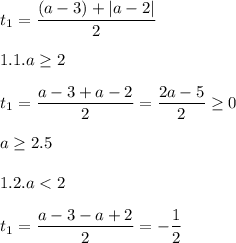
$\displaystyle t_1=\frac{(a-3)+|a-2|}{2}\\\\1.1.a\geq 2\\\\t_1=\frac{a-3+a-2}{2}=\frac{2a-5}{2}\geq 0\\\\a\geq 2.5\\\\1.2. a$

значит при а≥2.5 мы получим один положительный корень (относительно t)

проверим второй корень

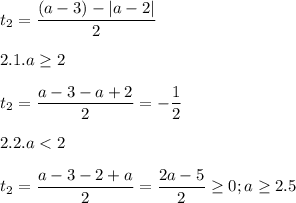
$\displaystyle t_2=\frac{(a-3)-|a-2|}{2}\\\\2.1. a\geq 2\\\\t_2=\frac{a-3-a+2}{2}=-\frac{1}{2}\\\\2.2. a$

тут положительных корней не получим.

значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5

выполним обратную замену

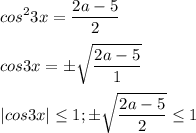
$\displaystyle cos^23x=\frac{2a-5}{2}\\\\cos3x=\pm\sqrt{\frac{2a-5}{1}}\\\\|cos3x|\leq 1; \pm\sqrt{\frac{2a-5}{2}}\leq 1$

рассмотрим положительный корень

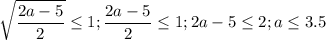
$\displaystyle \sqrt{\frac{2a-5}{2}}\leq 1; \frac{2a-5}{2}\leq 1; 2a-5\leq 2; a\leq 3.5$

рассмотрим отрицательный корень

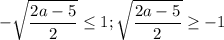
$\displaystyle -\sqrt{\frac{2a-5}{2}}\leq 1; \sqrt{\frac{2a-5}{2}}\geq -1$

выполняется для всех а≥2.5

Собираем все вместе 2,5≤а≤3,5

4,4(65 оценок)

Ответ:

nikzaytsev2001

07.06.2021

{x=6

y=2

z=5

Объяснение:

Метод Крамера:

Δ= $\left[\begin{array}{ccc}2&1&-3\\1&-3&2\\3&-4&1\end{array}\right]$ =2*(-3)*(-1)+1*2*3+(-3)*1*(-4)-(-3)*(-3)*3-1*1*(-1)-2*2*(-4)=14

Δx= $\left[\begin{array}{ccc}-1&1&-3\\10&-3&2\\5&-4&-1\end{array}\right]$ =(-1)*(-3)*(-1)+1*2*5-3*10*(-4)-(-3)*(-3)*5-1*10*(-1)+1*2*(-4)=84

Δy= $\left[\begin{array}{ccc}2&-1&-3\\1&10&2\\3&5&-1\end{array}\right]$ =2*10*(-1)+(-1)*2*3+(-3)*1*5-(-3)*10*3-(-1)*1*(-1)-2*2*5=28

Δz= $\left[\begin{array}{ccc}2&1&-1\\1&-3&10\\3&-4&5\end{array}\right]$ =2*(-3)*5+1*10*3+(-1)*(-4)*1-(-1)*(-3)*3-1*1*5-2*10*(-4)=70

x=Δx/Δ=84/14=6

y=Δy/Δ=28/14=2

z=Δz/Δ=70/14=5

Метод Гаусса

$\left[\begin{array}{cccc}2&1&-3&-1\\1&-3&2&10\\3&-4&1&5\end{array}\right]$

Делим первую строку на 0,5(r1/0.5)

$\left[\begin{array}{cccc}1&0.5&-1.5&-0.5\\1&-3&2&10\\3&-4&1&5\end{array}\right]$

Далее r3-3r1 и r2-r1

$\left[\begin{array}{cccc}1&0.5&-1.5&-0.5\\0&-3,5&3,5&10,5\\0&-5,5&3,5&6,5\end{array}\right]$

Следующая итерация r2/(-3.5)

$\left[\begin{array}{cccc}1&0.5&-1.5&-0.5\\0&1&-1&-3\\0&-5,5&3,5&6,5\end{array}\right]$

cледующий шаг r1-0.5r2 И r3+5.5r2

$\left[\begin{array}{cccc}1&0&-1&1\\0&1&-1&-3\\0&0&1&5\end{array}\right]$

Последний шаг r1+r3 r2+r3

$\left[\begin{array}{cccc}1&0&0&6\\0&1&0&2\\0&0&1&5\end{array}\right]$

{x=6 y=2 z=5

Матричный метод

A= $\left[\begin{array}{ccc}2&1&-3\\1&-3&2\\3&-4&1\end{array}\right]$

Δ= $\left[\begin{array}{ccc}2&1&-3\\1&-3&2\\3&-4&1\end{array}\right]$ =2*(-3)*(-1)+1*2*3+(-3)*1*(-4)-(-3)*(-3)*3-1*1*(-1)-2*2*(-4)=14

Находим миноры:

M11= $\left[\begin{array}{cc}-3&2\\-4&-1\end{array}\right]$ =11

M12= $\left[\begin{array}{cc}1&2\\3&-1\end{array}\right]$ =-7

М13= $\left[\begin{array}{cc}1&-3\\3&-4\end{array}\right]$ =5

M21= $\left[\begin{array}{cc}1&-3\\-4&-1\end{array}\right]$ =-13

M22= $\left[\begin{array}{cc}2&-3\\3&-1\end{array}\right]$ =7

M23= $\left[\begin{array}{cc}2&1\\3&-4\end{array}\right]$ =-11

M31= $\left[\begin{array}{cc}1&-3\\-3&2\end{array}\right]$ =-7

M32= $\left[\begin{array}{cc}2&-3\\1&2\end{array}\right]$ =7

M33= $\left[\begin{array}{cc}2&1\\1&-3\\\end{array}\right]$ =-7

A11=11 A12=7 A13=5

A21=12 A22=7 A23=11

A31=-7 A32=-7 A33=-7

A*= $\left[\begin{array}{ccc}11&7&8\\13&7&11\\-7&-7&-7\end{array}\right]$

A*т= $\left[\begin{array}{ccc}11&13&-7\\7&7&-7\\5&11&-7\end{array}\right]$

A-1= A*т/Δ= $\left[\begin{array}{ccc}11/14&13/14&-1/2\\1/2&1/2&-1/2\\5/14&11/14&-1/2\end{array}\right]$

X=A-1*B

B= $\left[\begin{array}{c}-1\\10\\5\end{array}\right]$

X= $\left[\begin{array}{ccc}11/14&13/14&-1/2\\1/2&1/2&-1/2\\5/14&11/14&-1/2\end{array}\right]$ * $\left[\begin{array}{c}-1\\10\\5\end{array}\right]$ = $\left[\begin{array}{c}11/14*(-1)+13/14*10-1/2*5\\1/2*(-1)-1/2*10-1/2*5\\5/14*(-1)+11/14*10-1/2*5\end{array}\right]$ = $\left[\begin{array}{c}-11/14+65/7-5/2\\-1/2+5-5/2\\-5/14+55/7-5/2\end{array}\right]$ = $\left[\begin{array}{c}6\\2\\5\end{array}\right]$