Ядро в алгебре — характеристика отображения f:A– B ,обозначаемая ker f отражающая отличие f от инъективного отображения, обычно — множество прообразов некоторого фиксированного (нулевого, единичного, нейтрального) элемента e. Конкретное определение может различаться, однако для инъективного отображения f множество ker f всегда должно быть тривиально, то есть состоять из одного элемента (как правило, нейтрального элемента из A.
Если множества A и B обладают некоторой структурой (например, являются группами или векторными пространствами), то ker f также должно обладать этой структурой, при этом различные формулировки основной теоремы о гомоморфизме связывают образ Im f и фактормножество A/ker f
Объяснение:
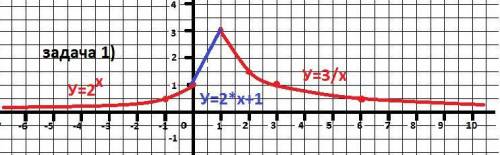
Задача 1) - рисунок к задаче в приложении.
При х=0 обе первых части графика совпадают в точке (0;1)
А третья функция: у = 3/х при х=1 равна
у(3) = 3/3 = 1.
Задача сводится провести прямую через две точки А(0;1) и В(1;3)
ДАНО: А(0;1), В(1;3)
НАЙТИ: Y = k*x + b
РЕШЕНИЕ
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(1-(3))/(0-(1))=2 - коэффициент наклона прямой
2) b=Аy-k*Аx=1-(2)*0= 1- сдвиг по оси ОУ
Уравнение Y(АВ) = 2*x+1 - функция на втором участке.
ОТВЕТ: а = 2 - коэффициент.
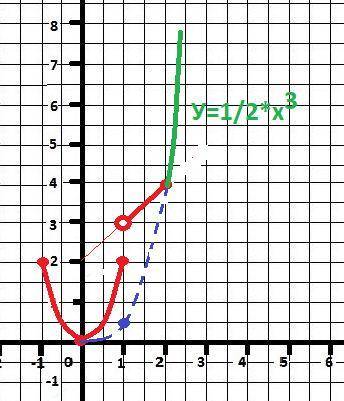
Задача 2) - рисунок в приложении.
При х = 2 на втором участке у = х + 2 = 4.
Задача сводится найти решение
y(2) = a*x³ = a*2³ = a*8 = 4
a = 4/8 = 0.5 = а - коэффициент - ответ.
222222222222222