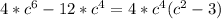
Определим общее число расстановок на пяти позициях 5 шариков:
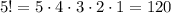
Однако, среди этих расстановок есть недопустимые (то есть те, при которых между зеленым и желтым шариком располагаются два или более шарика). Найдем число недопустимых расстановок.
Найдем число недопустимых размещений зеленого и желтого шарика. Их можно просто перечислить:
1) зеленый на 1-ом месте, желтый на 4-ом месте
2) зеленый на 1-ом месте, желтый на 5-ом месте
3) зеленый на 2-ом месте, желтый на 5-ом месте
4) зеленый на 4-ом месте, желтый на 1-ом месте
5) зеленый на 5-ом месте, желтый на 1-ом месте
6) зеленый на 5-ом месте, желтый на 1-ом месте
В каждом из этих случаев оставшиеся три шарика могут размещаться на свободных местах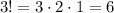 
Таким образом, всего имеется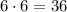 
недопустимых расстановок.
Значит, допустимых расстановок имеется:
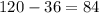
ответ: 84
По условию:
1 собака + 2 кошки => 60 минут
4 собака + 2 кошки => 20 минут
Если в первом случае увеличить количество собак и кошек в 3 раза, то им всем вместе потребуется в 3 раза меньше времени:
3 собаки + 6 кошек => 20 минут
Теперь у нас есть две ситуации, занимающие одно и то же время: 4 собака + 2 кошки едят сосиски за 20 минут и 3 собаки + 6 кошек едят сосиски за 20 минут. Приравняем:
4 собака + 2 кошки = 3 собаки + 6 кошек
1 собака = 4 кошки
То есть, одна собака может заменить 4 кошки.
Видоизменим первое условие, увеличив число животных в два раза и сократив время в два раза:
2 собаки + 4 кошки => 30 минут
Подставим соотношение "1 собака = 4 кошки":
2 собаки + 1 собака => 30 минут
3 собака => 30 минут
Но если собак будет в три раза меньше, то времени будет затрачено в три раза больше:
1 собака => 90 минут
ответ: 90 минут
4c в шестой степени - 12с в 4 степени=4c^4(c^2-3)