Объяснение:
1.
График - парабола.
Этот график получается из графика
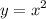 ,
,
смещением на 1 единицу влево
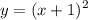 ,
,
а затем смещением вниз на 4 единицы
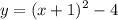
2.
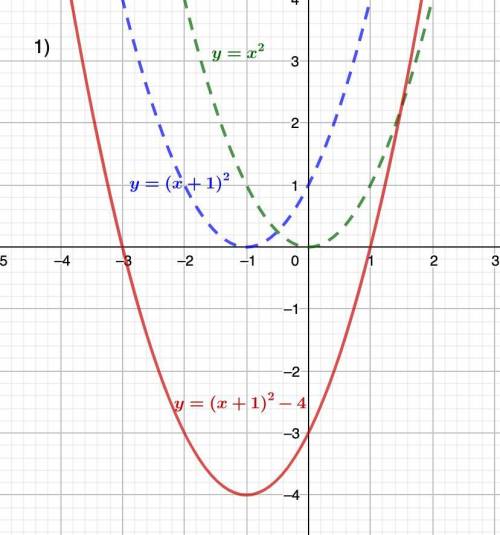
Это график линейной функции, содержащей переменную под знаком модуля.
Сначала построим график у=х.
Сдвинем его на 3 единицы вниз, при этом ось 0х график пересечет в точке х=3 (уголочек в центре графика)
у=х-3
Чтобы часть графика отобразилась зеркально относительно оси 0х, заключим правую часть под знак модуля.
у=|х-3|
Сместим на 1 единицу вниз
у=|x-3|-1
Отобразим часть ниже оси 0х зеркально, то есть еще раз заключим под знак модуля.
у=||x-3|-1|
3.
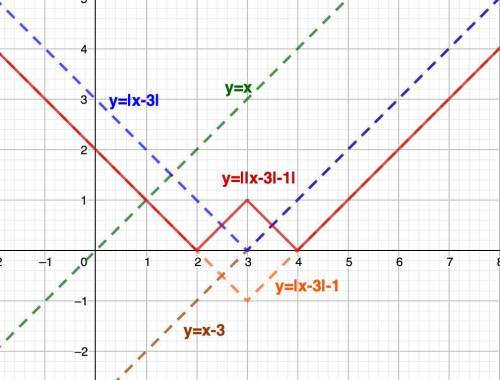
Это гипербола получается из графика
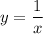
сдвигом на 2 единицы вправо
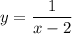 ,
,
а затем на 3 единицы вверх
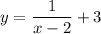
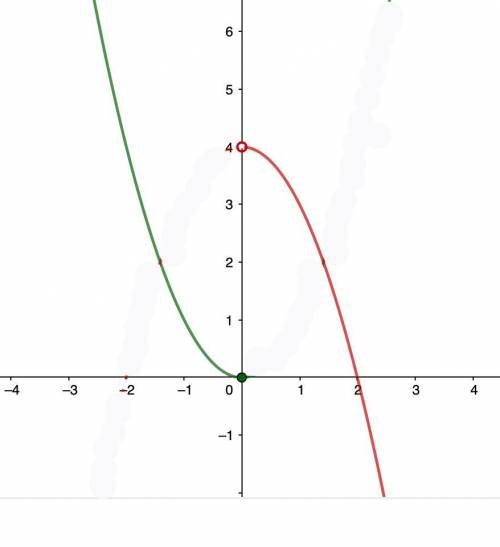
4.
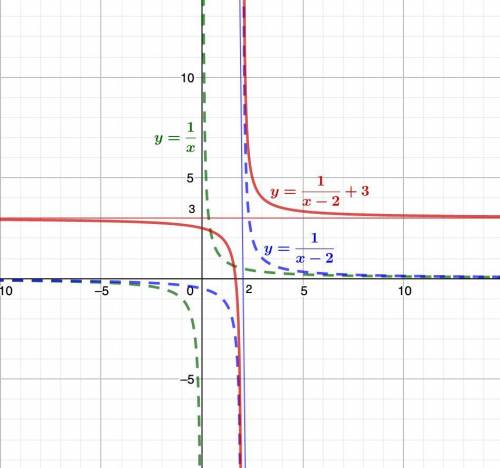
Это кусочная функция.
Слева- часть параболы, ветви вверх, вершина в точке (0,0):
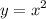
Справа - часть параболы, ветви вниз, вершина сдвинута на 4 единицы вверх:
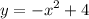
Функция будет иметь вид:
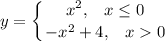
Не люблю задания, в которых больше одной задачи. Но эти задачи симпатичные, допускающие не совсем стандартные рассуждения. Вот ради этих рассуждений я и берусь за решение задач.
4. 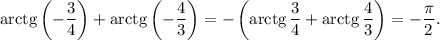 ответ: - 1
ответ: - 1
Объяснение: арктангенс трех четвертых и арктангенс четырех третьих - это острые углы в прямоугольном треугольнике с катетами 3 и 4, поэтому их сумма равна 90 градусам.
6. арктангенсы одной второй и одной третьей меньше 45 градусов, поэтому их сумма лежит в первой четверти. Воспользуемся формулой
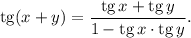
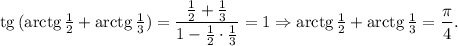
Осталось сосчитать синус полученного угла и возвести результат в квадрат. ответ: 0,5
5. Арксинус 4/5 - это острый угол (лежащий против катета, равного 4) прямоугольного треугольника ABC с катетами BC=4 и AC=3 и гипотенузой AB=5. Нас интересует половина этого угла, поэтому рисуем биссектрису AD , которая поделит катет BC на отрезки CD=3/2 и DB=5/2, пропорциональные боковым сторонам. В прямоугольном треугольнике ADC катеты AC=3; CD=3/2. Чтобы упростить вычисления, рассмотрим подобный ему треугольник A'D'C' с катетами A'C'=2 и C'D'=1 и гипотенузой A'D'=корень из 5. Интересующий нас угол, равный половине арксинуса 4/5 - это угол A' этого треугольника, а второй острый угол равен арктангенсу 2. Поэтому
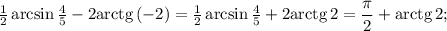
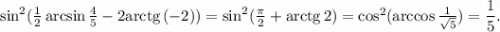
ответ: 0,2
-6×0,1²-10×0,1×(-0,2)-9×(-0,2)² =-6×0,01-0,2-9×0,04=-0,06-0,2-0,36=0,62