Наиболее верен ответ под буквой А - эта формула задаёт функцию, это легко подтвердить - мы можем подставить вместо V и а, y и х. Мы увидим привычную школьникам форму y=x^3 - степенная функция.
Под буквой Б ответ неправильный, так как аргумент функции - независимая величина, а значит, в нашем случае это будет а.
Под буквой В ответ неправильный, так как если мы уменьшим каждую сторону в два раза, то получим величину, в 2^3=8 раз меньшую, чем исходная.
Под буквой Г ответ неправильный, так как 4^3=64
ответ: А
В решении.
Объяснение:
1) Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
а) у = 2х -3 А(-1; -5)
-5 = 2*(-1) - 3
-5 = -2 - 3
-5 = -5, принадлежит.
б) у = 2х -3 В(0; 3)
3 = 2*0 - 3
3 ≠ -3, не принадлежит.
в) у = 2х -3 С(-4; 7)
7 = 2*(-4) - 3
7 ≠ -11, не принадлежит.
г) у = 2х -3 Д(2,5; 2)
2 = 2*2,5 - 3
2 = 5 - 3
2 = 2, принадлежит.
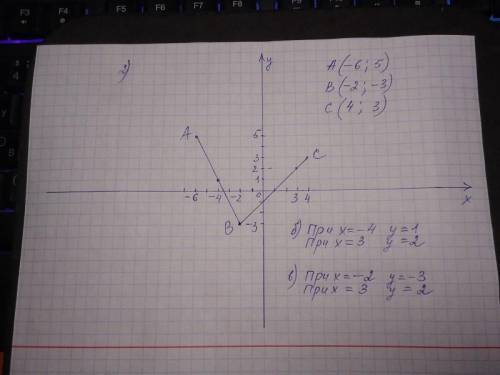
2) На фото.
3)
а) Область определения - это проекция графика на ось Ох, все значения х, при которых функция существует. Согласно рисунка, функция существует при значениях х от -2 до 7, значит, область определения D(f) = [-2; 7].
Кружки на концах графика закрашены, это значит, что значения х= -2 и х=7 входят в область определения функции, скобки квадратные.
б) Область значений функции - это проекция графика на ось Оу, означает, в каком интервале существуют значения функции. Согласно рисунка, эти значения от у= -2 до у= 4,8, значит, область значений
Е(f) = [-2; 4,8], скобки также квадратные.
в) f(3) - запись говорит о том, что нужно найти значение у при х=3. Согласно рисунка, при х=3 у=3.
г) f(x) = 2, запись говорит о том, что нужно найти значение х при у=2. Согласно рисунка, при х=2 у=2.
д) Точка одна, координаты (6,5; 0).
е) Определить значения х, при которых у < 0, это график ниже оси Ох.
у < 0 при х∈(6,5; 7), то есть при х от 6,5 до 7.
ж) Определить значения х, при которых у > 0, это график выше оси Ох.
у > 0 при х∈(-2; 6,5), то есть при х от -2 до 6,5.
а) равны
б) равны
с) равны
д) 2(3x-1) и 6x-2= 6х-2 и 6х-2. соответственно равны
е) x+y-2x+3y и 4y-x= -х+4у и 4y-x. соответственно равны
f) равны
h)5x-2y+x и -2y+6x= 6х-2у и -2y+6x. соответственно равны
i)x^2+2y И 2(x^2+y)-x^2= 2х^2 -x^2 +2y= x^2 +2y. равны
j)3x(x-y) И 3y(y-x)= 3х^2 -3xy и 3у^2 -3x. не равны
k)(x-y)y и (x-y)x= ху-у^2 и x^2-yx. не равны
l)(x+y)x и (x-y)x= x^2 +yx и x^2-xy. не равны