Решите ур-е sin2x=sin(p/2+x) найдите все корни этого ур-я принадлежащие к отрезку -7p/2,-5p/2

👇

Ответ:

tematal

25.03.2023

2sinxcosx = cosx
2sinxcosx - cosx = 0
cosx ( 2sinx - 1 ) = 0
cosx = 0 2sinx - 1 = 0
x = p/2 + pn 2sinx = 1
sinx = 1
x = (-1)^n p\2 + pn

4,5(76 оценок)

Открыть все ответы

Ответ:

nikitenkov20066

25.03.2023

25 (км/ч)

Объяснение:

Расстояние против течения - Sпр.теч. = 100 км

Время против течения - tпр.теч. = 4часа

Расстояние по течению - Sпо теч. = 150 км

Время по течению - tпо теч. = 5 часов

На сколько км/ч скорость течения реки меньше собственной скорости лодки?

Пусть Vc. - собственная скорость лодки, а Vт. - скорость течения реки.

⇒ Vпо теч.=Vс. + Vт., Vпр.теч. = Vс. - Vт.

Чтобы найти скорость, нужно расстояние разделить на время:

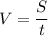
$\displaystyle V=\frac{S}{t}$

Найдем скорости по течению и против течения:

Vпр.теч. = 100:4 = 25 (км/ч)

Vпо теч. = 150:5 = 30 (км/ч)

Получим систему:

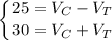
$\displaystyle \left \{ {{25=V_C-V_T} \atop {30=V_C+V_T}} \right.$

Сложим уравнения и найдем Vc.:

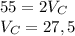
$\displaystyle 55=2V_C\\V_C=27,5$

Собственная скорость лодки Vс.=27,5 км/ч

Найдем скорость течения реки:

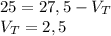$\displaystyle 25=27,5-V_T\\V_T=2,5$ (км/ч)

Найдем, на сколько км/ч скорость течения реки меньше собственной скорости лодки:

27,5 - 2,5 = 25 (км/ч)

4,4(24 оценок)

Ответ:

Бос2017

25.03.2023

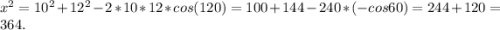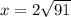
1) По теореме косинусов x^2=10^2+12^2-2*10*12*cos(120)=100+144-240*(-cos60)=244+120=364. ; $x=2\sqrt{91}$

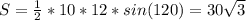
$S=\frac{1}{2}*10*12*sin(120)= 30\sqrt{3}$

2) По теореме синусов 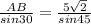$\frac{AB}{sin30}= \frac{5\sqrt{2}}{sin45}$ ; AB=5.

3) Из теоремы косинусов следует, что 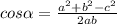$cos\alpha =\frac{a^2+b^2-c^2}{2ab}$ Пусть напротив стороны длиной 6 см лежит угол α, напротив отрезка длиной 8 см лежит угол 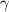$\gamma$ , а напротив стороны длиной 11 см лежит угол β.

Тогда cosα=(8^2+11^2-6^2)/(2*8*11)= 149/176. Значит, α - острый угол.

cosγ=(6^2+11^2-8^2)/(2*6*11)= 93/132

Следовательно, 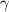$\gamma$ -острый угол.

Аналогично 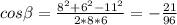$cos\beta=\frac{8^2+6^2-11^2}{2*8*6}=- \frac{21}{96} \\$ <0 Значит, β - тупой угол.

Таким образом, треугольник - тупоугольный.

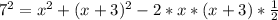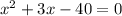4) Пусть треугольник имеет стороны x, x+3 и 7, где угол между сторонами x и x+3 равен 60. По теореме косинусов $7^2=x^2+(x+3)^2-2*x*(x+3)*\frac{1}{2}$ . Выходит, что x^2+3x-40=0 ;

x=-8 или x=5. Значит, x=5. Тогда периметр треугольника равен 5+(5+3)+7=20 см.

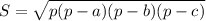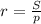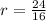5) Пусть a=4 см, b=13 см и c=15 см. Найдем площадь треугольника по формуле Герона. $S=\sqrt{p(p-a)(p-b)(p-c)}$ , где p-полупериметр треугольника. Тогда p=16 см и $S=\sqrt{16*12*3*1}$ =24. Радиус вписанной окружности можно найти по формуле $r=\frac{S}{p}$ . Тогда $r=\frac{24} {16}$ =1,5.

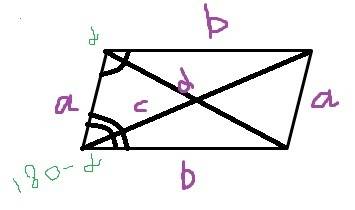
6) Пусть медиана к стороне длиной 4 см равна с. Достроим треугольник до параллелограмма с диагоналями равными 4 и 2*с.

В параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон. Докажем этот факт. Ясно, что с^2=a^2+b^2-2*a*b*cosα. Аналогично d^2=a^2+b^2-2*a*b*cos(180α)=a^2+b^2+2*a*b*cosα. Сложим полученные равенства. Выходит, что c^2+d^2=2(a^2+b^2), ч.т.д.

Тогда имеем: 2*(5^2+7^2)=(2*c)^2+4^2

Решив это уравнение получим, что 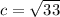$c=\sqrt{33}$