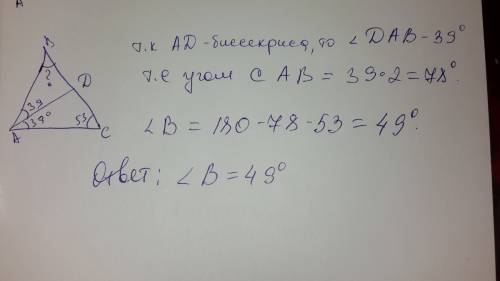
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3



1) эту последовательность можно представить как арифметическую прогрессию с разностью d = 1, первым членом a1 = 30
количество членов этой арифм.прогрессии ---количество всех натуральных двузначных чисел не меньших 30 (т.е. больших либо равных 30), начиная с 30 и заканчивая 99 ---их (99-30)+1 = 70
Sn = (a1+an)*n/2
S70 = (30+99)*70/2 = 129*35 = 4515
или по другой формуле
Sn = (2a1+(n-1)*d)*n/2
S70 = (2*30+(69)*1)*70/2 = (60+69)*35 = 129*35 = 4515
2)
для решения этого неравенства нужно оценить выражение в первой скобке ---понять больше или меньше оно нуля...
3V7 - 4V5 ? 0
V(9*7) - V(16*5) ? 0
V63 - V80 ? 0
80 > 63 => V80 > V63 => V63 - V80 < 0 т.е. 3V7 - 4V5 < 0
произведение двух множителей, один из кот. <0 по условию должно быть >0 => второй множитель тоже <0
0.15 -2x < 0
2x > 0.15
x > 0.3