№1
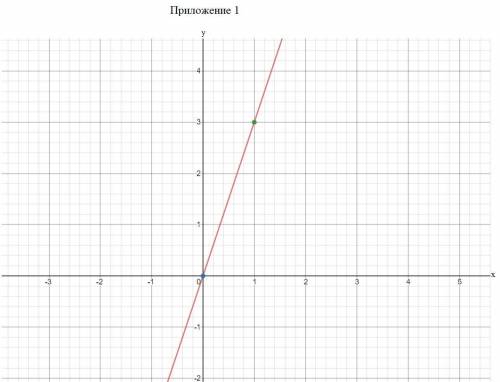
a) y=3x
График данной функции - прямая линия. Следовательно, для ее построения потребуются две точки.
Найдем эти точки:
x=0; y=3*0=0
x=1; y=3*1=3
Строим график(см. приложение 1).
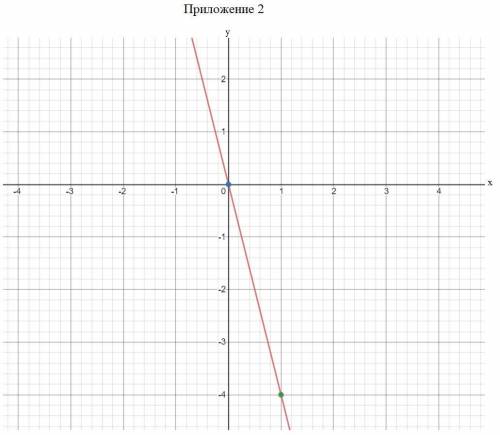
б) y=-4x
Решается аналогично a:
x=0; y=0;
x=1; y=-4
Строим график(см. приложение 2).
№2
y=7x
Чтобы узнать, принадлежат ли данные точки графику функции, надо подставить их координаты в функцию.
A(0;1) => x=0; y=1
1=7*0 - неверно, значит точка A не принадлежит графику функции
B(-2;14) => x=-2; y=14
14=7*(-2)
14=-14 - неверно, значит точка B не принадлежит графику функции
C(0,7;4,9) => x=0,7; y=4,9
4,9=7*0,7
4,9=4,9 - верно, значит точка C принадлежит графику функции
D(-1,5;-10,5) => x=-1,5; y=-10,5
-10,5=(-1,5)*7 - верно, значит точка D принадлежит графику функции
ответ: A,B - не принадлежат; C,D - принадлежат
Если раскрыть скобки, то получим квадратное уравнение с параметром а. Но делать мы этого не будем. Просто вспомним, что решение квадратного уравнения это
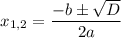
То есть если один корень будет рациональным, то и второй тоже. Ситуации, что один корень будет иррациональным, а второй нет - невозможна. Поэтому задача становится решить исходное уравнение в целых числах и определить то самое а по условию.
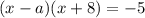
Произведение двух чисел равно 5. Это будет тогда, когда одно из них равно 5 по модулю, а второе 1 по модулю (все это потому что 5 - простое число и его делители это 1 и 5 со знаками). При этом у них должны быть разные знаки. То есть получаем 4 случая => 4 аналогичные системы (все они в совокупности), из которых мы и найдем а.
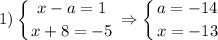
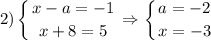
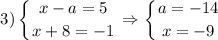
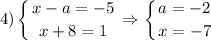
Здесь, кстати, ничего удивительного. У уравнения два корня, просто для одного корня, например, первая скобка равна 1, а вторая равна -5. А для второго корня первая скобка равна 5, а вторая -1. И это все при одном значении параметра.
В итоге у нас есть 2 подходящих значения параметра
a=-14, a=-2. Выбираем наименьшее из них, это a=-14.
ответ: -14.