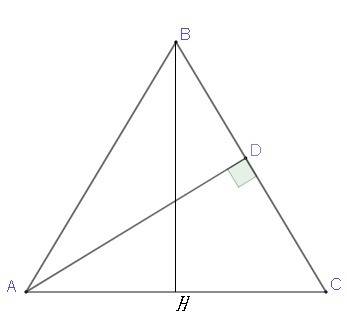
Дано: ABC - равнобедренный треугольник; AC = 12 см; AD = 9.6 см; AB=BC.
Найти: Рabc.
Из прямоугольного треугольника ADC по теореме Пифагора найдем CD
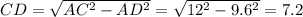см.
Пусть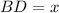 
, тогда 
.
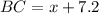Рассмотрим прямоугольный треугольник BHC найдем высоту BH к стороне основания AC; AH=CH=AC/2=6 см.
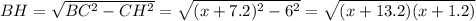
Площадь равнобедренного треугольника равна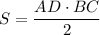 
, с другой стороны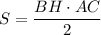 
Приравнивая площади, получим AD * BC = BH * AC.
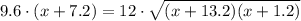
После возведения в квадрат обе части уравнения и упрощений с подобными членами вы должны получить следующее квадратное уравнение
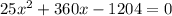
Корни которого: 
- не удовлетворяет условию
см
Тогда 
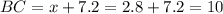см
Pabc = AB + BC + AC = 10 + 10 + 12 = 32 см
ответ: 32 см.
Объяснение:
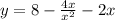
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
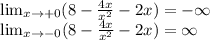
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
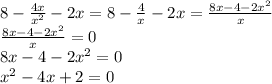
Решаем квадратное уравнение, находим точки пересечения с осью х:
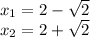
Находим точки экстремума (производная равна нулю).
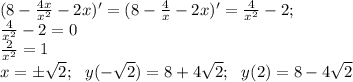
Для нахождения точек перегиба находим вторую производную
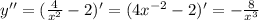
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
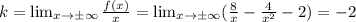
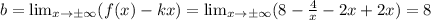
Наклонная асимптота есть:
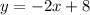
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
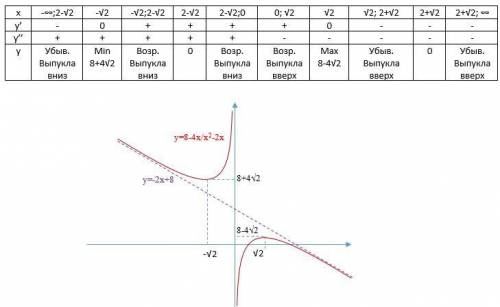
1) (1+9)*(9-9)=0
2) 635%
х100%
х=63*100/5=1260га