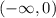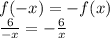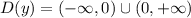
 получается с растягивания графика
получается с растягивания графика 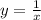 (обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности.
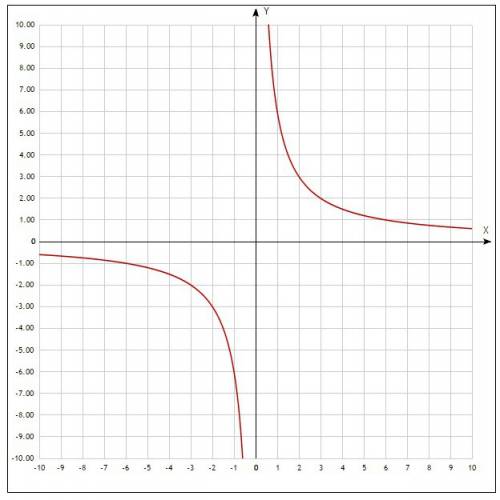
(обратная пропорциональность) вдоль оси у в 6 раз. Это означает, что у данной функции, многие свойства такие же как и у обратной пропорциональности. тоже является гиперболой.
тоже является гиперболой.
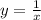 принимает отрицательные значения на луче
принимает отрицательные значения на луче 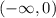 то и
то и  принимает отрицательные значения на луче
принимает отрицательные значения на луче