Question

Сумма 8 и 6 члена арифметической прогрессии=16 а произведение 2 и 12=-36. найти разность и первый член прогрессий.

Answer 1

Из условия: $\displaystyle \left \{ {{a_8+a_6=16} \atop {a_2a_{12}=-36}} \right.$

Используем формулу n-го члена арифметической прогрессии $a_n=a_1+(n-1)d$, имеем

$\displaystyle \left \{ {{a_1+7d+a_1+5d=16} \atop {(a_1+d)(a_1+11d)=-36}} \right.~~~\Rightarrow~~~\left \{ {{a_1+6d=8} \atop {(a_1+6d-5d)(a_1+6d+5d)=-36}} \right.\\ \\ (8-5d)(8+5d)=-36\\ \\ 64-25d^2=-36\\ \\ 25d^2=100\\ \\ d^2=4\\ \\ d=\pm2$

Если d=2, то $a_1=8-6d=8-6\cdot2=-4$

Если d=-2, то $a_1=8-6\cdot(-2)=8+12=20$

ответ: a₁=-4 и d=2 или a₁=20 и d=-2.

Answer 2

Выразим a₆, a₈, a₂ и a₁₂ через формулу n-ого члена арифметической прогрессии.

aₙ = a₁ + (n-1)×d, где d - разность арифметической прогрессии, n - номер

$a_6 = a_1 + 5d\\\\a_8 = a_1 + 7d\\\\a_2 = a_1 + d \\\\a_{12} = a_1 + 11d$

Составим систему из двух уравнений

$\left \{\begin{array}{lcl} {{a_6+a_8=16} \\ {a_2\cdot a_{12}=-36}}\end{array} \right. \\\\\\\left \{\begin{array}{lcl} {{a_1+5d+a_1+7d=16} \\ {(a_1+d)\cdot (a_1 + 11d)=-36}}\end{array}\right.\\\\\\\left \{\begin{array}{lcl}{{2a_1+12d=16\;\;|:2} \\ {((a_1+6d)-5d)\cdot ((a_1 + 6d)+5d)=-36}}\end{array} \right.\\\\\\\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {(a_1+6d)^2-25d^2=-36}}\end{array} \right.$

$\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {\underbrace{(a_1+6d)^2}_{8^2}-25d^2=-36}}\end{array} \right.\\\\\\\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {25d^2=100}}\end{array} \right.\\\\\\\left \{\begin{array}{lcl} {{a_1+6d=8} \\ {d=\pm 2}}\end{array} \right.$

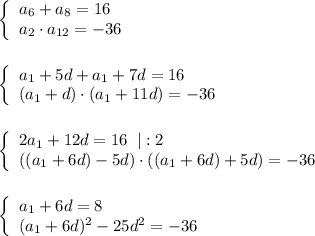
Если d = 2, то a₁ = 8 - 6d = 8 - 12 = -4

Если d = -2, то a₁ = 8 + 12 = 20

ответ: Если d = -2, то a₁ = 20, а если d = 2, то a₁ = -4