Пусть, для определённости, d>=c>=b>=a. Тогда всю дробь можно переписать в виде:
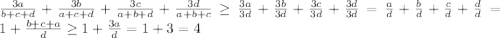
Что и требовалось доказать.
Пояснение: Выражение после первого знака неравенства получается, если взять наименьший знаменатель, а это d+d+d=3d.
Выражение после второго знака неравенства получается оттого, что мы берём наибольший числитель(то есть b+c+a=a+a+a=3a).
Выражение после третьего знака неравенства справедливо так как a>=d, то есть a/d>=1. Отсюда 3*(a/d)>=1*3=3
P.S. Если что-то непонятно, то не стесняйся спрашивать)


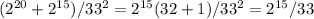
4 = t * (t - 2)
t^2 - 2t - 4 = 0
(t^2 - 2t + 1) = 5
(t - 1)^2 = 5
t = 1 + sqrt(5) -- второй корень будет меньше 0
|x + 1| = 1 + sqrt(5)
x + 1 = +-(1 + sqrt5)
x = sqrt(5) или x = -2-sqrt(5)