* * * * * * * * * * * * * * * * * * * * * * * * *
Решите систему уравнений { 3xy -x =5 ; 3xy -y= 4
ответ: (x₁ ; y₁) = ( -5/3 ; -2/3 ) ; ( x₂ ; y₂) = (1 ; 2) .
Объяснение:
{ 3xy -x =5 ; 3xy -y= 4 . ⇔ { 3xy -x-(3xy -y) = 5 - 4 ; 3xy -x =5 . ⇔
{ y=x+1 ; 3xy - x =5 .⇔ { y=x+1 ; 3x(x+1) - x -5 =0 .⇔ { y=x+1 ; 3x²+2x -5 =0 .
3x²+2x -5 =0
D₁= D/4 =( 2/2)² - 3*(-5) =1²+15 =16 = 4² ; x = (-1 ± √D₁)/3
⇒ x₁ = (-1 -4) /3 = - 5/3 ⇒ y₁ = x₁+1 = -5/3+1 = -2/3
x₂ = (-1 +4) /3 = 1 ⇒ y₂ = x₂+1 =1 +1 = 2 .
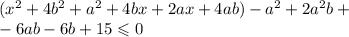
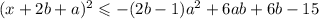
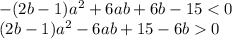
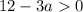
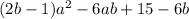должен принимать только положительные значения. Как известно, так будет, если: 1. Коэффициент при a^2 положительный и 2. Дискриминант отрицательный.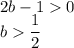
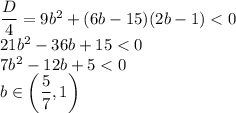
1) ищем производную
2) приравниваем её к нулю и решаем уравнение
3) полученный корни ставим на числовой прямой и проверяем знаки производной на каждом промежутке
4) пишем ответ
Начали:
1) производная = 5^(х² + 12x + 38) ln5·(2x + 12)
2)5^(x² + 12x + 38) ln5·(2x + 12) = 0
2x + 12 = 0
2x = -12
x = -6
3) -∞ - -6 + +∞
4) x = -6 - это точка минимума
у min= 5^(36 -72 +38)= 5^2 = 25