у = kx + b
так как график проходит через начало координат, b = 0.
подставим координаты точки М в уравнение
4 = k * (-2.5)
Отсюда найдем k = 4/(-2.5) = -1.6
то есть искомая формула линейной функции у = -1,6х
Теперь, чтоб найти точку пересечения этого графика с прямой 3х-2у - 16 = 0, решим систему из 2 линейных уравнений
у = -1,6х
3х-2у - 16 = 0
подставив у из первого уравнения во второе, получим
3х + 3,2х - 16 = 0
6,2х = 16
х = 16/6,2= 80/31
тогда у = -1,6 *80/31 = -128/31
То есть искомая точка пересечения (80/31; -128/31)
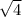 <√6<
<√6<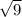
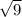 <√11<
<√11<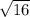
а) Область определения: x∈R
б) Вертикальных асимптот нет, функция везде определена.
в) Пересечение с осями.
с Ох:
y=0
x⁴ -10x₂ +9 =0
Замена: x² = t
t² - 10t +9 =0
t₁+t₂ = 10
t₁*t₂ = 9
t₁ = 9
t₂ = 1
x₁₂ = √9 = +-3
x₃₄ = √1 = +-1
Пересечение Oy:
x=0
y(0) = 0⁴ + 10*0² + 9= 9
г) Функция четная
д) Асимптоты наклонные:
y = kx+b
k =
Наклонных асимптот нет
2) Исследуем функцию с первой производной.
y' = (x⁴ -10x² +9)' = 4x³ -20x
Приравняем производную к нулю:
4x³ -20x = 0
4x(x² - 5) = 0
x = 0 или x =+-√5
Посмотрим как ведет себя функция на этих отрезках.(см. №1)
x = +-√5 - точка минимума, ymin = -16
x = 0 - точка максимума y max = 9
3) Исследуем функцию с второй производной.
y'' = 12x² - 20
Приравняем к 0
12x²-20 = 0
x = +-√20/12
Функция знак не меняет - значит точек перегиба нет.
4) Сам график.
см №2