Объяснение:
Если -4 ; 2 ; -2 ; 0,2 ; ... является арифметической прогрессией, то каждый последующий член должен отличаться от предыдущего на одно и то же число.
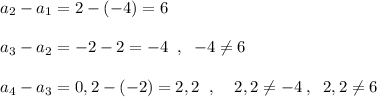
Как видим, это свойство арифм. прогрессии не выполняется .
Если считать, что задана геометрическая прогрессия, то каждый последующий член должен быть равен предыдущему члену, умноженному на одно и то же число q .
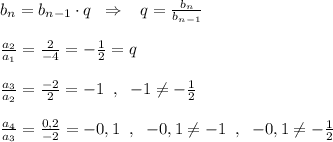
Здесь тоже не выполняется свойство геом. прогрессии, так как число q должно быть одним и тем же.
Поэтому вычислить 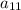ни 
, ни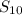 
вычислить невозможно .
Объяснение: y=12*sin(x) + 5*cos(x) -4;
Сделаем преобразование с выражением: 12*sin(x) + 5*cos(x) =
=√(12²+5²) × ((12×sin(x))/ √(12²+5²) + ( 5×cos(x)/√(12²+5²)) =
...= 13× ((12sin(x)/13 + (5×cos(x)/13) = 13×((cosβ×sin x + sinβ×cosx) =
= 13×sin(x+β);
Где cosβ=(12/13), a sinβ=(5/13);
Область определения функций y=cos(x+β) и y=cos(x) будет множество всех действительных чисел, потому что β=arccos(12/13)
есть определенное число.
Функция; y=12×sin(x) + 5×cos(x) -4= 13×sin(x+β) -4=13×sin(α) -4;
где α=(х+β);
Итак максимальное значение данной функции:
y=13×sinα-4= 13×1-4=13-4=9;
Минимальное значение функции:
y=13×sinα-4= 13×(-1) -4=-13-4=-17;
Здесь применяли максимальное и минимальное значение sinα: -1;1.
ответ: область значений функции [-17;9}.
На 3: 13^n = (12 + 1)^n = 12*(...) + 1 - степень даёт остаток 1 при делении на 3. Тогда 13^n - 1 делится на 3 при всех n
На 6: 13^n - нечётное число, отсюда 13^n - 1 - четное. Число делится на 3 и на 2 -> делится на 6.
На 13: число на 13 не делится, т.к. ни 7 не делится на 13, ни 13^n-1 не делится на 13, а 13 - простое число.
а), б), в)