1) Указать формулу общего ( n- ого) члена арифметической прогрессии -3 ; 1.5
2) В геометрической прогрессии первый член равен 3 , второй член равен 12 , а последний член равен 3072. Сколько членов в прогрессии ?
3) (bn) - геометрическая прогрессия , в которой b5 = 81 , q= 3/4 .
1) а1=-3
а(n)=-3+4,5*(n-1)
а(n) =-3+4,5n-4,5
a(n) =-7,5+4,5n
a(n)=4,5n-7,5
2) b1=3
b2=12
q=12/3=4
b(n) =3072
3072=3*4^(n-1)
3072/3=4^(n-1)
1024=4^(n-1)
4^5=4^(n-1)
5=n-1
n=6
6 членов в прогрессии
3)b5=81
b5=b1*(3/4)^4
81=b1*(81/256)
b1=256
S5=b1*(q^5-1)/(q-1)
256*((243/1024)-1)/(-1/4)
-243+1024=781

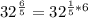
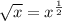
![\sqrt[3]{x} =x^{\frac{1}{3}}](/tpl/images/0503/0859/f093d.png)
![32^{ \frac{1}{5}} =\sqrt[5]{32}](/tpl/images/0503/0859/6c7d6.png)
![\sqrt[5]{32}=\sqrt[5]{2^{5}}](/tpl/images/0503/0859/ad486.png)
![\sqrt[5]{2^{5}}=2^{\frac{5}{5}}=2](/tpl/images/0503/0859/67bfa.png)
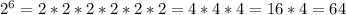
а(n)=-3+4,5*(n-1)
а(n) =-3+4,5n-4,5
a(n) =-7,5+4,5n
a(n)=4,5n-7,5
2) b1=3
b2=12
q=12/3=4
b(n) =3072
3072=3*4^(n-1)
3072/3=4^(n-1)
1024=4^(n-1)
4^5=4^(n-1)
5=n-1
n=6
6 членов в прогрессии
3)b5=81
b5=b1*(3/4)^4
81=b1*(81/256)
b1=256
S5=b1*(q^5-1)/(q-1)
256*((243/1024)-1)/(-1/4)
-243+1024=781