у=2х-7 искомое уравнение.
Объяснение:
Составьте уравнение вида y = kx+ b, график которого проходит через данные точки C (-3;-13) и D (1;-5)
Формула, при которой можно построить уравнение прямой по двум точкам:
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)
C (-3;-13) и D (1;-5)
х₁= -3 у₁= -13
х₂=1 у₂= -5
Подставляем данные в формулу:
(х-(-3)/(1-(-3)=(у-(-13)/(-5)-(-13)
(х+3)/4=(у+13)/8 перемножаем крест-накрест, как в пропорции:
8(х+3)=4(у+13)
8х+24=4у+52
-4у= -8х+52-24
-4у= -8х+28
4у=8х-28/4
у=2х-7 искомое уравнение.
Тангенс угла наклона касательной равен производной в точке касания к графику функции.
tgα = y'(x).
1) y = 0,2x^2 + 2x - 4, A(2; 0,8).
Проверяем - принадлежит ли точка данной функции.
0,2*2² + 2*2 - 4 = 0,8. Да, принадлежит.
Находим производную: y' = 0,2*2x + 2.
y'(2) = 0,2*2*2 + 2 = 2,8.
ответ: tgα = 2,8.
2) y = -3x^2 - x + 5, А(-2; -5).
Аналогично проверяем - точка А на кривой (парабола).
y' = -6x - 1,
y'(-2) = -6*(-2) - 1 = 12 - 1 = 11.
ответ: tgα = 11.
3) y = (x^2 - 1)/(x - 5), A(3; 3 2/3). (Ели так дано задание)
В этой задаче сложное решение, так как точка А не лежит на кривой.
Производная : y' = (2x(x - 5) - 1*(x^2 - 1))/(x - 5)^2) = (x^2 - 10x + 1)/((x - 5)^2).
Производная в точке касания хо: (xо^2 - 10xо + 1)/((xо- 5)^2).
Получим уравнение касательной проходящей через точку A(3;3 2/3):
3 2/3 = ((xо^2 - 10xо + 1)/((xо- 5)^2))(3 - хо) + ((xо^2 - 1)/(xо - 5)).
Решение затруднено, так функция - кубическая.
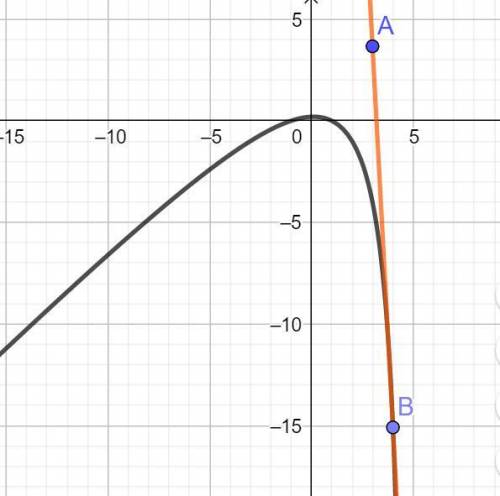
Ориентировочно решение найдено графически в программе ГеоГебра: у = -18,76х + 59,95.
График приведен во вложении.
при любых
Рассмотрим функцию
Найдем производную , и интервалы убывания , возрастания .
функция возрастает
функция убывает
И теперь очевидно что что бы уравнение имело три разных корня , нужно что бы всегда было возрастания функций , иными словами нужно вычислить значение
ответ