кр-03. вариант 1. ответы:
№ 1. 1) 3х(х3 – 4х + 6) = 3x4 – 12x2 + 18x; 2) (х – 3)(2х + 1) = 2x2 + x – 6x – 3;
3) (4а – 7b)(5а + 6b) = 20a2 + 24ab – 35ab – 42b2 = 20a2 – 11ab – 42b2;
4) (у + 2)(у2 + у – 8) = y3 + y2 – 8y + 2y2 + 2y – 16 = y3 + 3y2 – 6y – 16
№ 2. 1) 5a² – 20ab = 5a(a – 4b) 2) 7x³ – 14x⁵ = 7x³(1 – 2x²)
3) 3a – 3b + ax – bx = (3a – 3b) + (ax – bx) = 3(a – b) + x(a + b) = (3 + x)(a² – b²)
№ 3. 4x(x + 3) = 0 ⇒ 1) x₁ = 0 2) x₂ = –3
№ 4. 5a2 – 21
№ 5. x = 5/4
№ 6. (3y +1)∙(6x – 8). подставили х, у, получили ответ: 4,4
№ 7. (2⁴)⁵ – (2³)⁶ = 2²⁰ – 2¹⁸ = 2¹⁸(2² – 1) = 2¹⁸(4 – 1) = 2¹⁸ ∙3.
значит кратно 3, так как в произведении есть множитель 3.
№ 8. (x + 3)(x + 5)
кр-03. вариант 2. ответы:
№ 1. 1) 5a(a4 – 6a² + 3) = 5a5 – 30a³ + 15a
2) (x + 4)(3x – 2) = 3x² – 2x + 12x – 8 = 3x² + 10x – 8
3) (6m + 5n)(7m – 3n) = 42m² – 18mn + 35mn – 15n² = 42m² + 17mn – 15n²
4) (x + 5)(x² + x – 6) = x³ + x² – 6x + 5x² + 5x – 30 = x³ + 6x² – x – 30
№ 2. 1) 18xy – 6x² = 6x(3y – x) 2) 15a6 – 3a⁴ = 3a⁴(5a² – 1)
3) 4x – 4y + cx – cy = x(4 + c) – y(4 + c) = (х – у)(4 + с)
№ 3. 3х(х + 3) = 0 ⇒ 1) x₁ = 0 2) x₂ = –3
№ 4. 13b² + 10(2b + 3)
№ 5. x = 33/5
№ 6. (8a – 1)(3b + 4). подставили a, b, получили ответ: –1,4
№ 7. 27⁴ – 9⁵ = 3¹² – 3¹⁰ = 3¹⁰(3² – 1) = 3¹⁰(3 – 1)(3 + 1) = 3¹⁰∙2∙4 = 8∙3¹⁰.
значит кратно 8, так как в произведении есть множитель 8.
№ 8. (х – 6)(х – 3)
 ;
;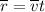 ;
;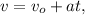 либо в векторном виде:
либо в векторном виде: 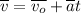 ;
;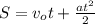 либо в векторном виде:
либо в векторном виде: 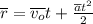 ;
;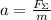 либо в векторном виде:
либо в векторном виде: 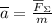 ;
; ;
;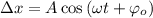 ;
;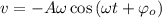 ;
; ;
;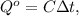 где
где 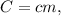 либо в удельном виде:
либо в удельном виде:  ;
;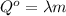 ;
;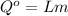 ;
; ;
; ;
;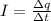 ;
;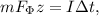 где
где  ;
;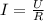 ;
;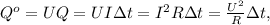
 ;
;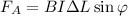 ;
; ;
;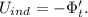
n=15 положит. членов последовательности
Проверим , найдём 15-ый и 16-ый члены посл-ти.