Дана арифметическая прогрессия -15, -12, ..., то есть a₁= -15, a₂= -12. Тогда
а) её разность:
d = a₂ - a₁ = -12 - (-15) = -12 + 15 = 3.
б) формула n-члена этой прогрессии :
a(n) = -15+3·(n-1)
в) выясним, содержится ли в этой прогрессии число 12:
a(n) = 12 или
-15+3·(n-1) = 12
3·(n-1) = 12 + 15
3·(n-1) = 27
n-1 = 27:3
n = 9+1=10∈N
Содержится под номером 10.
г) Так как d=3 >0, то в этой прогрессии бесконечное количество положительных членов. В самом деле:
a(n) = -15+3·(n-1)>0
3·(n-1)>15
n-1>15:3
n>5+1
n>6
Начиная с 7-члена арифметической прогрессии все члены положительные. Так как множество натуральных чисел N бесконечно, то положительных членов арифметической прогрессии бесконечно.
25 км/ч скорость лодки в неподвижной воде.
Объяснение:
Плот плывет со скоростью течения реки , следовательно:
30 : 5 = 6 ч . - время , которое он затратил
6-1 = 5 ч. - затратила лодка на путь туда-обратно
Лодка:
Собственная скорость - х км/ч
По течению:
Скорость - (х+5) км/ч
Расстояние - 60 км
Время - 60 /(х+5) ч.
Против течения :
Скорость - (х-5) км/ч
Расстояние - 60 км
Время - 60/(х-5) ч.
Уравнение.
60/(х+5) + 60/(х-5) = 5
(60(х-5) +60(х+5) ) / (х²-25) = 5 * (х²-25)
60х - 300 +60х +300 = 5(х²-25)
120 х = 5х²-125
120х -5х² + 125 =0 ÷(- 5)
х²-24х- 25=0
D= (-24)² - 4 *(-25) = 576+100=676
D > 0 - два корня
х₁= (24-√676) /2 = (24-26)/2 = -2/2=-1 - не удовл. условию задачи
х₂= (24+26 )/2= 50/2 =25 - собственная скорость лодки

б)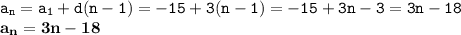
в)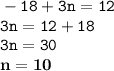
г)получается, что количество положительных членов бесконечно
ответ: а)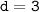 ; б)
; б) 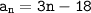 ; в)
; в)  ; г) бесконечное множество
; г) бесконечное множество