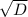) / 2a = (-4 + 10) / 2*1 = 6/2 = 3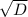) / 2a = (-4 - 10) / 2*1 = -7
Гоша все верно написАл. Я немного поясню.
Из второго уравнения
1/x^2 = 1 - y^2;
x^2 = 1/(1 - y^2); подставляю в первое
1/(1 - y^2) + 1/y^2 = 3;
y^2 + 1 - y^2 = 3*y^2*(1 - y^2);
y^4 - y^2 + 1/3 = 0; это - биквадратное уравнение, подстановкой z = y^2 получается простое квадратное
z^2 - z + 1/3 = 0; вещественных решений у этого уравнения нет. Проще всего это показать так - можно добавить и вычесть 1/4
z^2 - z + 1/4 - 1/4 + 1/3 = 0;
(z - 1/2)^2 + 1/12 = 0; ясно, что слева стоит число больше 0 при любых z, поэтому вещественных решений нет.
(х - 5)·√(5х - 4 - х²) = 0
ОДЗ: 5х - 4 - х² ≥ 0
найдём корни уравнения
- х² + 5х - 4 = 0
D = 25 - 16 = 9
√D = 3
x₁ = (-5 - 3):(-2) = 4
x₂ = (-5 + 3):(-2) = 1
График функции 5х - 4 - х² квадратная парабола веточками вниз, и выше оси х находится в интервале между 1 и 4, поэтому неравенство 5х - 4 - х² ≥ 0 верно, при х∈[1;4]
Итак ОДЗ: х∈[1;4]
Теперь будем решать уравнения
(х - 5)²·(5х - 4 - х²) = 0
Используем корни уравнения - х² + 5х - 4 = 0 и представим
- х² + 5х - 4 = (-1)(х -1)(х - 4)
(х - 5)²·(-1)(х -1)(х - 4) = 0
Корни этого уравнения х₁ = 4, х₂ = 1, х₃ = 5
Корень х₃ = 5 не подходит т.к. х = 5∉ОДЗ
Среднее арифметическое корней: (1 + 4):2 = 2,5
D=16+4*21=100
x1=(-4+10)/2=3
x2=(-4-10)/2=-7