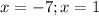
Объяснение:
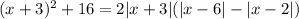
Выделим в левой части полный квадрат. Для этого прибавим к обеим частям уравнения выражение 
и перенесем слагаемое 
в левую часть:
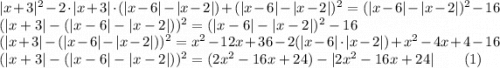
1) 
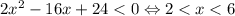
Тогда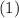 
примет вид
Левая часть неотрицательна. Правая часть, учитывая рассматриваемый интервал, строго отрицательна. Значит, корней на данном интервале нет.
2) 
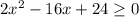
Возможны 2 случая:
2.1)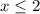 
Тогда 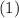примет вид
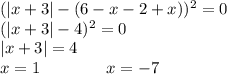
Оба корня принадлежат рассматриваемому интервалу, а значит являются корнями исходного уравнения.
2.2) 
Тогда 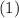примет вид
То есть корень не принадлежит рассматриваемому интервалу.
Пусть коэффициент пропорциональности равен k , тогда градусные меры внешних углов треугольника равны 3k , 4k и 5k .
Сумма внешних углов треугольника равна 360⁰ .
3k + 4k + 5k = 360
12k = 360
k = 30
3 * 30 = 90⁰ - 1 угол
4 * 30 = 120⁰ - 2 угол
5 * 30 = 150⁰ - 3 угол
Внутренние углы треугольника являются смежными с каждым из соответствуюшим ему внешним углом . Так как сумма смежных углов равна 180⁰, то внутренние углы треугольника равны :
90⁰ , 60⁰ , 30⁰ .
Сумма внутренних углов треугольника равна 180⁰, значит внутренние углы относятся как 3 : 2 : 1
3 * 30 = 90 2 * 30 = 60 1 * 30 = 30
ответ : 3 : 2 : 1
x^2+kx+15=0 (Знак ^ означает возведение в степень. В данном случае в квадрат) Если это так, то решение:
Подставим корень уравнения и вычислим k
3^2+k*3-15=0
3k=15-9
3k=6
k=2
Теперь решим квадратное уравнение:
x^2+2x-15=0
По теореме, обратной теореме Виета x1=3 x2=-5
ответ: k=2 x2=-5