В решении.
Объяснение:
d) |4 - x| < 5
Схема:
4 - x < 5; 4 - x > -5
-x < 5 - 4 -x > -5 - 4
-x < 1 -x > -9
x > -1 x < 9
(знак неравенства меняется при умножении или делении на минус).
Решение неравенства: х∈(-1; 9).
Неравенство строгое, скобки круглые.
е) |3x - 9| + 2 > 7
|3x - 9| > 7 - 2
|3x - 9| > 5
Схема:
3x - 9 > 5 3x - 9 < -5
3x > 5 + 9 3x < -5 + 9
3x > 14 3x < 4
x > 14/3 x < 4/3
Решение неравенства: (-∞; 4/3)∪(14/3; +∞).
Неравенство строгое, скобки круглые.
f) |3x + 2| - 1 >= 10
|3x + 2| >= 10 + 1
|3x + 2| >= 11
Схема:
3x + 2 >= 11 3x + 2 <= -11
3x >= 11 - 2 3x <= -11 - 2
3x >= 9 3x <= -13
x >= 3 x <= -13/3
Решение неравенства: (-∞; -13/3]∪[3; +∞).
Неравенство нестрогое, скобки квадратные, а знаки бесконечности всегда с круглой скобкой.
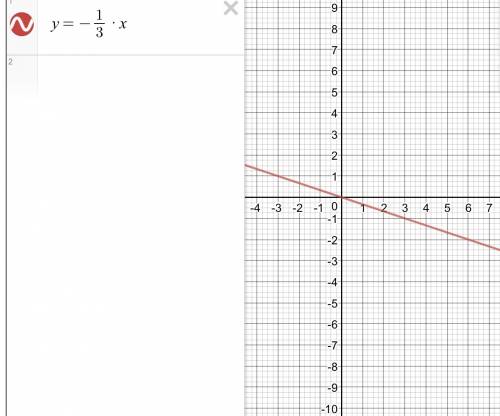
а). у=-1/3*х- прямая пропорциональность. График-прямая, проходящая через начало координат. И возьми еще 1 любую точку. Пусть х=6, у=-2. Проведи через точки (0;0) и (6;-2) прямую. Это график
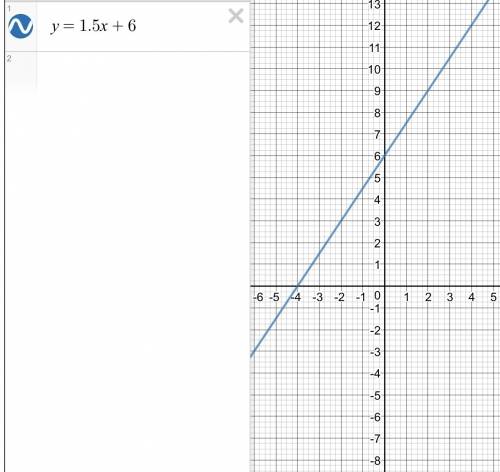
b). у=1,5х+6 - линейная функция. график - прямая. Чтобы построить возьми любые 2 точки если х=0, то у=6. х=-2, у=-2*1,5+6=-3+3=3
Через точки (0;6) и (-2;3) проведи прямую. Это график.
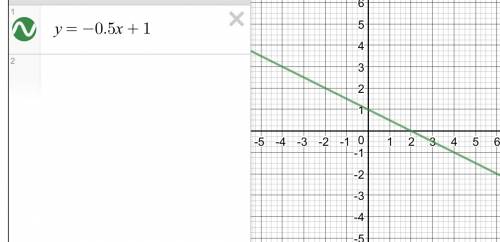
в) Аналогично у=-0,5х+1 тоже линейная функция. Если х=0, то у=1. Если х=6, то у=-2
Через точки (0;1) и (6;-2) проведи прямую. это график

S2=πR²
S=S2-S1=π(R²-r²)
r² min=122500 r²max=123201
R² min=324900 R² mfx=326041
R²-r² min 202400 mfx 202840
635536<π(R²-r²)<638946