Решение
Через вершину B проведем прямую, параллельную AC, продлим медиану AА₁ до пересечения с этой прямой в точке T.
Из равенства треугольников А₁BT и A А₁C (по стороне и двум прилежащим углам: B А₁ = А₁C, т. к. A А₁ — медиана,
∠B А₁T = ∠A А₁C — вертикальные, ∠ А₁BT = ∠ А₁CA — накрест лежащие при параллельных прямых AC, BT и секущей BC) следует, что BT = AC и A А₁ = KT. Из подобия треугольников
AML и MBT (по двум углам: ∠MAL = ∠BTА₁,
∠ALB = ∠LBT — накрест лежащие при параллельных
прямых AC, BT и секущих BL, AT) следует,
что AL : BT = AL : AC = AM : MT. Так как АА₁ = А₁T,
то AM : MT = 1 : 7.
Тогда AL : AC = 1 : 7, а AL : LC = 1 : 6.
решение во вкладыше
Данное уравнение не имеет целых корней.
Используем метод Феррари:
уравнение вида
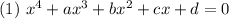
с замены 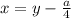
приводим к виду:
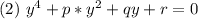
где:
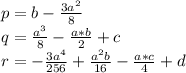
добавим и вычтем из левой части уравнения 2 выражение 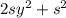 , где s - некоторое число:
, где s - некоторое число:

получим:
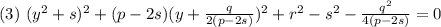
Пусть s - корень уравнения
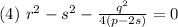
Тогда уравнение 3 примет вид:
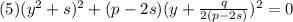
Избавляемся в уравнении 4 от знаменателя:
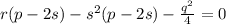
Раскроем скобки и получим:
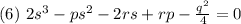
Уравнение 6 называется кубической резольвентой уравнения 4 степени.
Разложим уравнение 5 на множители:
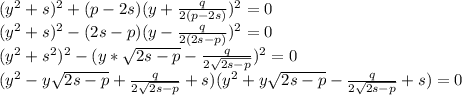
Получим два квадратных уравнения:
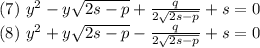
Применяем этот метод для решения уравнения
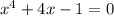
Перепишем уравнение в полном виде:
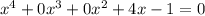
коэффиценты:
a=0
b=0
c=4
d=-1
определяем p,q и r:
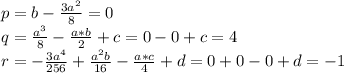
ищем s:
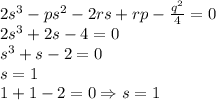
подставляем p,q,r и s в квадратные уравнения 7 и 8:
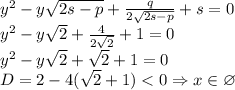
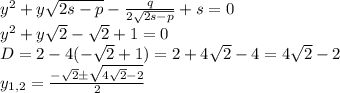
Теперь находим x:
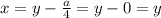
ответ: 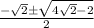
во втором х+2
в обоих х+(х+2)
значит ответ 3)