x^3=4y
y=x
y=(x^3)/4 и у=х
найдем точки пересечения
система:
y=x
y=(x^3)/4
x=(x^3)/4
4x=x^3
4=x^2
x1=2
x2=-2
и общая точка-начало координат, через которую проходит прямая и гипербола (0;0)
Площадь:
0 2 0 2
S(-x+(x^3)/4)dx+ S(x-(x^3)/4)dx=(-(x^2)/2+(x^4)/16))/+((x^2)/2-(x^4)/16))/= (-0+0-(-4/2+16/16))+(4/2-16/16-0-0)=2-1+2-1=2
-2 0 -2 0
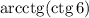
Известно соотношение:
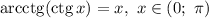
Кроме этого, известно, что основной период котангенса равен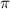 
:
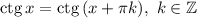
Таким образом, аргумент 6 нужно заменить некоторым аргументом вида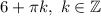 
, чтобы с одной стороны котангенсы этих аргументов были равны, а с другой стороны полученный аргумент удовлетворял формуле для простого нахождения арккотангенса от котангенса.
Запишем неравенство:
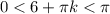
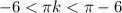
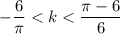
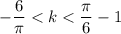
Выполним оценку обеих частей неравенства:
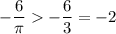
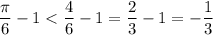
Получим:
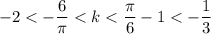
Или записывая соотношение для k:
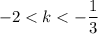
Единственное подходящее целое значение: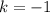 
.
Запишем:
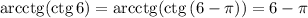
Действительно, 
, арккотангенс может принимать такое значение.
ответ: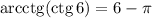 
2sinxcosx+
2sinxcosx+2
2cosx(sinx+1)=0
cosx=0 sinx=-1
x=
2) 8sinx-7cosx=0 /:cosx
8tgx-7=0
8tgx=7
tgx=7/8
x=arctg7/8+