Question

Выражения. два примера. решите . отзовитесь кто решит.

Answer 1

1) y-2. ОДЗ: y≠2

2) a-1. ОДЗ: a≠1

Объяснение:

№1. (y+2+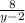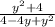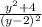$\frac{8}{y-2}$):$\frac{y^2+4}{4-4y+y^2}$=$\frac{y^2-4+8}{y-2}$:$\frac{y^2+4}{(y-2)^2}$=$\frac{(y^2+4)(y-2)^2}{(y-2)(y^2+4)}$=y-2. ОДЗ: y≠2

№2. (a+1+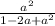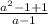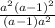$\frac{1}{a-1}$):$\frac{a^2}{1-2a+a^2}$=$\frac{a^2-1+1}{a-1}$:$\frac{a^2}{(a-1)^2}$=$\frac{a^2(a-1)^2}{(a-1)a^2}$=a-1. ОДЗ: a≠1

ОДЗ - область допустимых значений. Т.е. когда мы сокращаем что-либо в числителе и знаменателе, то мы можем потом включить это число в решения. То есть, например, в первом номере мы сокращаем скобку y-2. Тем самым мы сознательно "пропускаем" в решения (если бы мы не просто упрощали, а решали такое уравнение). Но эта скобка стоит у нас в знаменателе. А знаменатель не может быть равен 0, т.к. на 0 делить нельзя. Значит нужно исключить решение такого уравнения: y-2=0, т.е. y не равен 2. В первом номере скобку y^2+4 мы не выносим в ОДЗ, потому что если мы будем решать такое уравнение: y^2+4=0, то увидим, что оно никогда не будет равно 0. Квадрат любого числа - число неотрицательное по определению, а неотрицательное+положительное=положительное, т.е. не равное 0. Поэтому эту скобку мы не вносим в ОДЗ. Во втором номере мы сокращаем a^2, т.е. автоматически "пропускаем" a=0. Значит нужно его исключить. Также мы сокращаем скобку a-1, значит нужно исключить решение уравнения a-1=0, т.е. a не равно 1.