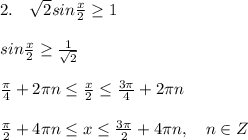
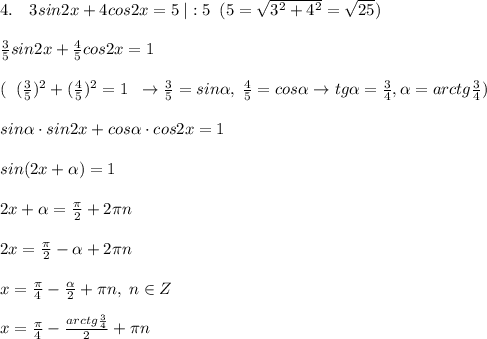



1)
1) Умножим обе части. = 3(х-1)-2(х+1)=6
2) Раскроем скобки. = 3х-3-2(х+1)=6 -> 3х-3-2х-2=6
3) Вычислим. = х-3-2=6 -> х-5=6
4) Переносим (-5) вправо. = х=6+5
5) Вычисляем и получаем: х = 11
ответ: х=11
2)
1) Раскроем скобки. = 2-х-2х+х(2)=(х+3)*(х-4) -> 2-х-2х+х(2)=х(2)-4х+3х-12
2) Уберём равные числа. = 2-х-2х=-4х+3х-12
3) Вычислим. = 2-3х=-4х+3х-12 -> 2-3х=-х-12
4) Переносим лишние числа (х) и (2) влево. = -3х+х=-12-2
5) Вычисляем. = -2х=-12-2 -> -2х=-14
6) Разделяем и получаем: х=7
ответ: х = 7
Разбор (2) после х, (2) означает степень.
Объяснение:
Обозначим искомые числа через х и у.
В условии задачи сказано, что среднее арифметическое двух этих чисел равно 20, а их среднее геометрическое составляет 12, следовательно, можем записать следующее соотношение:
х + у = 40;
х * у = 144.
Решаем полученную систему уравнений.
Подставляя во второе уравнение значение у = 40 - х из первого уравнения, получаем:
х * (40 - х) = 144;
40х - х^2 = 144;
х^2 - 40x + 144 = 0;
x = 20 ± √(400 - 144) = 20 ± √256 = 20 ± 16;
х1 = 20 + 16 = 36;
х2 = 20 - 16 = 4.
Находим у:
у1 = 40 - х1 = 40 - 36 = 4;
у2 = 40 - х2 = 40 - 4 = 36.
ответ: искомые числа 4 и 36.