1) Точки пересечения с осями.
- с осью Оу: х = 0, у =0^3+0^2-16*0-16 = -16, точка (0; -16).
- с осью Ох: у = 0.
x^3+x^2-16x-16 = 0.
Преобразуем заданное уравнение:
у =x^3+x^2-16x-16 = х²(х+1)-16(х+1) = (х²-16)(х+1) = (х-4)(х+4)(х+1).
у = 0, (х-4)(х+4)(х+1) = 0.
Отсюда получаем 3 корня уравнения: х₁ = 4, х = -4, х = -1.
2) Для того, чтобы найти экстремумы, нужно найти производную и приравнять её нулю и корни этого уравнения будут экстремумами данной функции:
y' = 3x² + 2 x - 16 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=2^2-4*3*(-16)=4-4*3*(-16)=4-12*(-16)=4-(-12*16)=4-(-192)=4+192=196;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√196-2)/(2*3)=(14-2)/(2*3)=12/(2*3)=12/6=2;
x₂=(-√196-2)/(2*3)=(-14-2)/(2*3)=-16/(2*3)=-16/6=-(8/3) ≈ -2,6667.
Значит, экстремумы в точках:
((-8/3); (400/27)),
(2, -36).
3) Определяем минимумы и максимумы функции и промежутки знакопостоянства.
Для этого находим значения производной вблизи критических точек.
х = -3 -2.667 -2 1 2 3
у' = 5 0 -8 -11 0 17.
Где производная меняет знак с + на - там максимум функции ((х=(-8/3); у= (400/27)), а где меняет знак с - на + там минимум функции (х=2; у=-36)).
Функция возрастает на промежутках -∞ < x < (-8/3) и 2 < x < +∞,
а убывает на промежутке (-8/3) < x < 2.
4) Найдем точки перегибов, для этого надо решить уравнение
y'' = 0 (вторая производная равняется нулю), корни полученного уравнения будут точками перегибов для указанного графика функции,
Решение
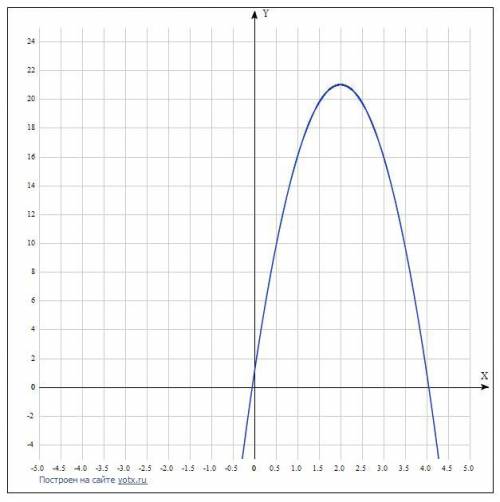
h=-5t²+20t+1 - надо понимать, что это квадратный трёхчлен - то есть перед нами уравнение параболы с ветвями вниз в пять раз уже стандартной параболы у= х², но у нас вместо у -h,а вместо х- t
Можно построить график и решить задачу, а можно алгебраически
1) h=16( подставляем в уравнение и решаем)
16=-5t²+20t+1 ;
5t²-20t+15=0; /:5
t²-4t+3=0
по теореме Виета t₁=1 t₂=3
ответ: Мяч поднимется на высоту через 1 секунду, ( отталкиваемся от слова "поднимется", потому что он опять будет на высоте 16м через 3 секунды, правда тогда он будет падать)
2)Тут надо найти ординату вершины
tв= -b/2a=-20/2*(-5)=2( абсцисса вершины , теперь подставим в уравнение и найдём hв)
hв=-5*2²+20*2+1=-20+40+1=21(м)
ответ: 21 метр- максимальная высота мяча
3) надо найти корни уравнения -5t²+20t+1 =0
D=20²-4*(-5)*1=400+100=500
√D=√500=10√5
Нам нужен положительный корень( время не может быть отрицательным!)
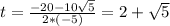 ≈2+1*2,2≈4,2 (c)
≈2+1*2,2≈4,2 (c)
Мяч пробудет в воздухе (2+√5 )секунд или ≈4,2 секунды
2)а(х-у)+4(х-у)=(а+4)(х-у)
3) х(3+х)=(х+4)(х-4)
х²+3х=х²-16
3х= - 16
х= -16/3 = - 5 1/3
4)3(а²+2аb+b²)-ab-3a²+2b²=3a²+6ab+3b²-ab-3a²+2b²=5ab+5b² или равно 5b(a+1)