Объяснение:
1. -х² - 4х + 4k = 0.
Для удобства разделим обе части на -1:
х² + 4х - 4k = 0.
Уравнение - квадратное. Найдем его дискриминант.
D = b² - 4ac = 4² - 4 × 1 × (-4k) = 16 + 16k.
Рассмотрим 3 возможных случая:
1) D < 0. Если D < 0, то корней нет:
16 + 16k < 0; 16k < -16 => k < -1. При k < -1 корней уравнение не имеет.
2) D = 0; 16 + 16k = 0 => k = -1. При таком значении параметра уравнение имеет единственный корень x = -b/2a = -4/(2×1)=-2.
3) D > 0. Если D > 0, (k>-1) то уравнение имеет два корня. Дальнейшее объяснение в первом вложении.
ответ: при k < -1 корней нет; при k = -1 корень x = -2; при k > -1 корни: х1 = -2 + 2√(k+1), х2 = -2 - 2√(k + 1).
2. Полное решение во втором вложении (решения справедливы для любого значения параметра k)
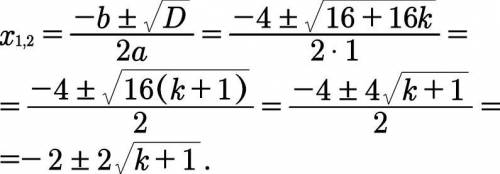

= ((x^2) - (y^2)) (x - y)^2 =
= ((4,5^2) - (3,5^2)) (4,5 - 3,5)^2 =
= (20,25 - 12,25) = 8
ответ: 8.