1) 5k+1
2) 36
3) 3186
Объяснение:
1) искомое натуральное число имеет вид: 5k+1, где k∈N₀ (k - натуральное, либо 0)
2) подставляем вместо k возможные значения:
а) k=0 ⇒ 5*0+1=1
б) k=1 ⇒ 5*1+1=6
в) k=2 ⇒ 5*2+1=11
г) k=3 ⇒ 5*3+1=16 и т.д.
замечаем, что каждое следующее число больше предыдущего на 5, то есть имеем арифметическую прогрессию, где а₁=1; d=5
чтобы определить сколько таких чисел (n) нужно, воспользуемся формулой n-го члена:
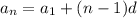
по условию у нас последний член не обязательно должен равняться 180, а только не должен его превышать (an≤180), значит запишем неравенство:
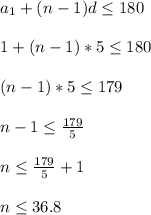
наибольшее значение n, удовлетворяющее неравенству равно 36.
Значит всего 36 таких чисел.
3) при полученном n, находим an
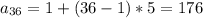
находим сумму по формуле:
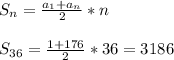
1) 5k+1
2) 36
3) 3186
Объяснение:
1) искомое натуральное число имеет вид: 5k+1, где k∈N₀ (k - натуральное, либо 0)
2) подставляем вместо k возможные значения:
а) k=0 ⇒ 5*0+1=1
б) k=1 ⇒ 5*1+1=6
в) k=2 ⇒ 5*2+1=11
г) k=3 ⇒ 5*3+1=16 и т.д.
замечаем, что каждое следующее число больше предыдущего на 5, то есть имеем арифметическую прогрессию, где а₁=1; d=5
чтобы определить сколько таких чисел (n) нужно, воспользуемся формулой n-го члена:
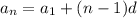
по условию у нас последний член не обязательно должен равняться 180, а только не должен его превышать (an≤180), значит запишем неравенство:
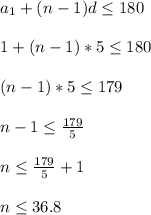
наибольшее значение n, удовлетворяющее неравенству равно 36.
Значит всего 36 таких чисел.
3) при полученном n, находим an
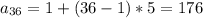
находим сумму по формуле:
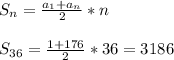
1) каким будет а7, если а1=15, S7= -21
S7=(a1+a7)/2*7
a7=S7*2/7-a1=-21*2/7-15=-21
2) а1, если а10= -30, S10= -20
S10=(a1+a10)/2*10
a1=S7*2/10-a10=-20*2/10-(-30)= 26
3) n, если a1= 7, an=26, d=1
an=a1+d*(n-1)
n=1+(an-a1)/d=1+(26-7)/1=20
4) a1, если a100=67, d= 2/3
a100=a1+d*99
a1=a100-d*99=67-99*2/3=1