верно , обратное нет
Объяснение:
пусть р - простое , рассмотрим остатки от деления р на 6 :
p = 6b + q , где 0 ≤ q ≤ 5 , если q = 2 , то p = 2(3b+1) , это
число четно и больше 2 , значит не простое , если q = 3 , то
p = 3(2q+1) , это число кратно 3 и больше 3 и значит также не
простое , если q = 4 , то p = 2( 3b + 2) , это число четно и
больше 2 и следовательно не простое , если q = 0 , то p
кратно 6 и не может быть простым , остаются 2 варианта : 1)
q= 1 , то есть p = 6b+1 и 2) q = 5 ⇒ p = 6b + 5 = 6b+6-1 =
6(b+1) - 1 = 6k -1 , а значит любое простое имеет вид : p = 6n±1
обратное утверждение неверно : например число 35 = 6·6 - 1
, но простым число 35 не является
Если каждое слагаемое делится на некоторое число, то и вся сумма делится на это число.
Если одно слагаемое делится на некоторое число, а другое слагаемое не делится на это число, то и вся сумма не делится на это число.
1.
Пусть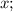 
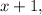
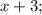
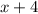- пять последовательных натуральных чисел, тогда их сумма равна:
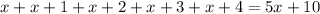
Очевидно, что каждое слагаемое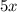 
и 
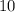делится на 5, а это означает, что вся сумма делится на 5.
Доказано.
2.
Пусть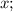 
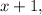
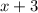- четыре последовательных натуральных числа, тогда их сумма равна:
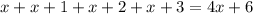
Очевидно, что первое слагаемое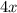 
делится на 4, а второе слагаемое 
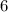не делится на 4, это означает, что вся сумма не делится на 4.
Доказано.
3.
Пусть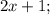 
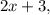
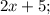
- четыре последовательных нечётных натуральных числа, тогда их сумма равна:
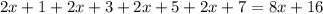
Очевидно, что каждое слагаемое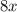 
и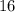 
делится на 8, а это означает, что вся сумма делится на 8.
Доказано.
4.
Пусть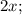 
; 
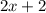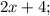
- четыре последовательных чётных натуральных числа, тогда их сумма равна:
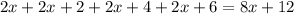
Очевидно, что каждое слагаемое 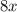и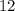 
делится на 4, а это означает, что вся сумма делится на 4.
Доказано.
2) c(c-2)(c+2)(c^2+c+1)= (c^2-2c)(c^2+c+1)=(c^3+2c^2-2c^2-c-4c)(c^2+c+1)=(c^3-4c)(c^2+c+1)=c^5+c^4+c^3-4c^3-4c^2-4c=c^5+c^4-3c^3-4c^2-4c/
4)4a^2(4a^2-a-2)
5)7x-14-x^2+2x=9x-14-x^2
6)(5a-ab)=(5c-cd)a(5-b)+c(5-d)
7)(3a-c)(3a+c)
8) 2(b^2-6bc+9c^2)=2(b-3c)^2