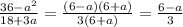
![D(y)=(0;\ 2].](/tpl/images/1860/7095/b9ff4.png)
Объяснение:
Для данной функции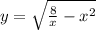 
есть два ограничения на область определения: первое, возникающее из-за квадратного корня и требующее, чтобы подкоренное выражение было неотрицательным, а также второе, возникающее из-за дроби, требующее, чтобы знаменатель дроби не был нулевым.
Получаем, что нужно решить неравенства:
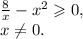
Решим первое:
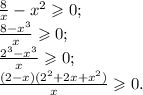
Разложив числитель на множители, мы можем решить неравенство методом интервалов. Выделим особые точки:
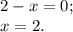
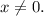
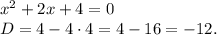
Корней нет. Точками для метода интервалов будут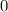 
, 
.
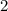Для всех точек левее 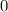значение выражения будет отрицательным.
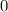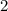Для точек между и значение выражения будет положительным.
Для точек правее 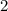значение выражения будет отрицательным.
Получаем, что решением неравенства будет промежуток чисел от 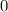до 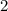. Поскольку неравенство нестрогое, промежуток должен включать свои границы, однако по причине наличия в системе неравенства 
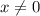, исключающего из решения левую границу промежутка, итоговый промежуток будет иметь вид: ![(0;\ 2].](/tpl/images/1860/7095/ec6e5.png)
Это решение и является областью определения функции, то есть ![x \in (0;\ 2].](/tpl/images/1860/7095/bee93.png)
