Пусть А - событие, которое состоится, если наудачу взятое двузначное число кратно 2, а В - событие, которое состоится, если это число кратно 7. Надо найти Р(А + В).Так как А и В - события совместные, то:
Р(А + В) = Р(А) + Р(В) - Р(АВ).
Двузначные числа - это 10, 11, . . . ,98, 99.
Всех их- 90 элементарных исходов. Очевидно, 45 из них кратны 2 (благоприятствуют наступлению А),
13 кратны 7 (благоприятствуют наступлению В) и ,наконец,7 кратны и 2, и 7 одновременно (благоприятствуют наступлению А×В). Далее по классическому определению вероятности:
Р(А) = 45/90 Р(В) = 13/90 Р(А×В) = 7/90
и, следовательно:
Р(А + В) = 45/90 + 13/90 - 7/90 = 51/90
ответ: 51/90
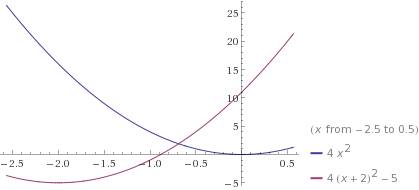
если для первого графика y = 4x^2 вершина находится в точке (0;0), то
ось симметрии параболы - ось OY (уравнение x=0)
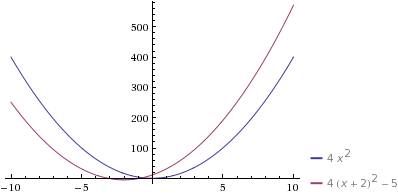
то для второго графика ось симметрии сместится влево на 2 (уравнение x = -2, все первое слагаемое обратится в 0 и получится y = -5), т.е. для второго графика вершина опустится вниз по оси OY на 5 единиц и сместится влево на 2 единицы по оси OX
координаты вершины новой параболы (-2;-5), ветви вверх и она в точности повторяет первый график (из новой точки---новой вершины), иными словами
новый график получится параллельным переносом исходного графика вниз по оси OY на 5 единиц и влево по оси OX на 2 единицы
tgx=2,4 U cox≠5/13⇒sinx≠12/13⇒tgx≠2,4-решения нет