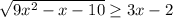
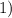
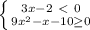
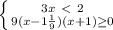
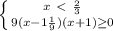
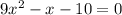
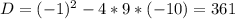
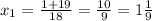
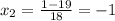
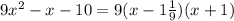
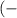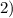
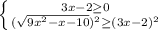
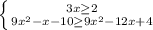
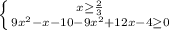
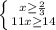
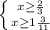
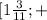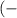∈ 
∞ ![;-1]](/tpl/images/0674/0179/c47ae.png)
∈ 
∞ 
∈ ∞ ∪ ∞ 
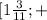2x−5y=12
Объяснение:
Подставим решение в каждое из представленных уравнений:
6x+11y=8
6*(-4)+11(-4)=8
-68≠8 не является решением уравнения
7x+8y=4
7*(-4)+8(-4)=4
-142≠4 не является решением уравнения
x−y=3
-4-(-4)=3
0≠3 не является решением уравнения
2x−5y=12
2*(-4)-5*(-4)=12
12=12 решение уравнения
7x−5y=3
7*(-4)-5(-4)=3
-8≠3 не является решением уравнения
45x−31y=13
45*(-4)-31*(-4)=13
-56≠13 не является решением уравнения
Значит уравнение, которое будет иметь решение (-4; -4) 2x−5y=12. Поскольку оба уравнение линейные значит решение будет единственным.
Значит система будет выглядит как:
2x−5y=12
−13x+8y=20
1)находим производную функции
2)приравниваем ее к 0
3)находим промежутки возрастания и убывания