
Пусть х - время, за которое Иван может вспахать все поле.
Тогда х+5 - время, за которое все поле может вспахать Григорий.
Примем всю площадь поля за 1.
Тогда 1/х - производительность Ивана.
1/(х+5) - производительность Григория.
1/х + 1/(х+5) - производительность Ивана и Григория, работающих вместе что соответствует 1/6.
Уравнение
1/х + 1/(х+5) = 1/6
Умножим обе части неравенства на 6х(х+5), чтобы избавиться от знаменателей.
6х(х+5)/х + 6х(х+5)/(х+5) = 6х(х+5)/6
6(х+5) + 6х = х(х+5)
6х+30 + 6х = + х^2 + 5х
х^2 - 7х - 30 = 0
D = 49 -4(-30) = 49 + 120 = 169
√D = √169 = 13
x1 = (7-13)/2 = -6/2 = -3 - не походит, поскольку время не может отрицательным.
х2 = (7+13)/2 = 20/2 = 10 часов - время, за которое Иван вспашет все поле.
ответ: 10 часов
Проверка
1) 1:10= 1/10 - производительность Ивана.
2) 1:6 = 1/6 - производительность Ивана и Григория, работающих вместе.
3) 1/6 - 1/10 = 5/30 - 3/30 = 2/30 = 1/15 - производительность Григория.
4/ 1 : 1/15 = 15 часов- за такое время Григория может выполнить всю работу.
5) 15-10=5 часов - на столько часов Иван выполнит работу раньше, чем Григорий.
Подробнее - на -
Объяснение:
При имеющихся исходных данным возможно 2 ответа:
1) b₁ = 6; q = 1/4;
1) b₁ = -6; q = -1/4;
Объяснение:
Член геометрической прогрессии с номером n вычисляется по формуле
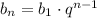
b₄ - b₂ = b₁ · q³ - b₁· q = b₁q(q² - 1)
b₆ - b₄ = b₁ · q⁵ - b₁· q³ = b₁q³(q² - 1)
По условию
b₁q(q² - 1) = -45/32 (1)
b₁q³(q² - 1) = -45/512 (2)
Преобразуем выражение (2)
b₁q³(q² - 1) = b₁q(q² - 1) · q²
В численном виде это можно записать как
-45/512 = -45/32 · q²
Откуда
q² = -45/512 : (-45/32)
q² = 1/16
q = ±1/4
Подставим q = 1/4 в выражение (1)
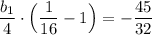
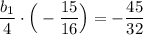
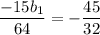
0.5b₁ = 3
b₁ = 6
Подставим q = -1/4 в выражение (1)
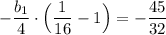
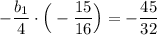

0.5b₁ = -3
b₁ = -6
Проверка:
1) b₁ = 6; q = 1/4
b₂ = 6 · 1/4 = 3/2
b₄ = 6 · 1/64 = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = 6 · 1/1024 = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512
2) b₁ = -6; q = -1/4
b₂ = -6 · (-1/4) = 3/2
b₄ = -6 · (-1/64) = 3/32
b₄ - b₂ = 3/32 - 3/2 = -45/32
b₆ = -6 · (-1/1024) = 3/512
b₆ - b₄ = 3/512 - 3/32 = -45/512