№ 1. (8 4/5 - 13,8 : 3 5/6) · 12/13 = 4 целых 4/5 = 4,8.
1) 13,8 : 3 5/6 = 138/10 : 23/6 = 69/5 · 6/23 = (3·6)/(5·1) = 18/5 = 3 3/5
2) 8 4/5 - 3 3/5 = 5 1/5 = 26/5
3) 26/5 · 12/13 = (2·12)/(5·1) = 24/5 = 4 4/5 = 4,8
№ 2. 1 - 0,15 : (11/12 - 0,75) = 0,1.
1) 11/12 - 0,75 = 11/12 - 3/4 = 11/12 - 9/12 = 2/12 = 1/6
2) 0,15 : 1/6 = 3/20 · 6/1 = (3·3)/(10·1) = 9/10 = 0,9
3) 1 - 0,9 = 0,1
№ 3. 8,3 - (3 5/12 - 1 1/3) : 5/12 = 3,3.
1) 3 5/12 - 1 1/3 = 3 5/12 - 1 4/12 = 2 1/12 = 25/12
2) 25/12 : 5/12 = 25/12 · 12/5 = 25/5 = 5
3) 8,3 - 5 = 3,3
Задание:
Решите уравнение.
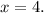
Объяснение:
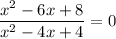
Дробь равна нулю, если числитель ему равен, а знаменатель — нет:
Так как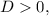 
то уравнение будет иметь два действительные корни, которые находятся по формуле:
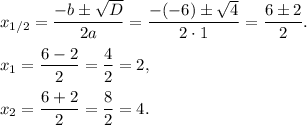
Но теперь надо проверить: подходят ли эти корни:
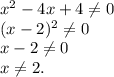
Теперь можем выяснить, что корень 
не подходит, так как не входит в ОДЗ.
Для точной проверки можно подставить корень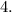 
Но это делать не обязательно:
Да, действительно корень 
является решением уравнения.
Также можно доказать, что корень 
не является решением:
Все правильно, так как на ноль делить нельзя.
(a1+a2+a3+a4)*5 = a5+a6+...+a12
an=a1+d(n-1)
a1+a2+a3+a4=a1+(a1+d)+(a1+2d)+(a1+3d)=4a1+6d
a5+a6+...+a12=8a1+60d
(4a1+6d)*5=8a1+60d
20a1+30d=8a1+60d
12a1=30d|:6
2a1=5d
a1=2,5d
a1+a2+...+a8 8a1+28d 8*2,5d +28d 20d+28d 48d
= = = = = 3
a1+a2+...+a4 4a1+6d 4*2,5d+6d 10d+6d 16d