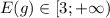Объяснение:
При решении этих задач самое важное узнать/понять какая функция из двух выше.
Задача 1. F(x) = 4 - прямая, Y(x) = x² - парабола
Рисунок к задаче в приложении.
Площадь это интеграл разности функций - верхней минус нижняя.
Находим пределы интегрирования - точки пересечения графиков: Y(x) = F(x)
х² = 4, x = √4 = ±2
a = -2, b= 2 - пределы интегрирования.
Пишем интеграл - площадь фигуры.
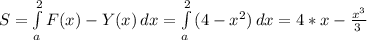
Вычисляем на пределах интегрирования.
S(b) = S(2) = 8 - 2 2/3 = 5 1/3
S(a) = S(-2) = -8 + 2 2/3 = -5 1/3
S = S(b)-S(a) = 5 1/3 - (-5 1/3) = 10 2/3 ед.²- площадь - ответ
Рисунок к задаче в приложении.
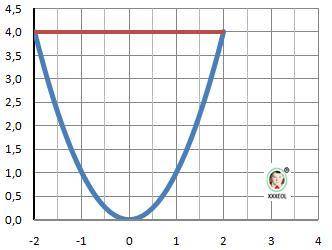
Задача 2. F(x) = 3*х и Y(x)=0 - функции,
a = 1, b = 5 - пределы интегрирования.
Площадь интеграл разности функций F(x)-Y(x).
![S=\int\limits^5_1 {3x} \, dx] =\frac{3*x^2}{2} =\frac{75}{2}-\frac{3}{2}=36](/tpl/images/1020/5456/723f0.png)
ОТВЕТ: Площадь 36 ед.²
Найдём дискриминант трёхчлена под корнем:
Дискриминант отрицателен, коэффициент при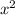
положителен, а значит, область определения функции 
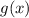равна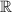 
(ведь под корнем должны быть только положительные числа).
Найдём минимальное значение многочлена под корнем с производной — обозначим его как функцию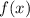
:
Тогда минимальное значение исходной функции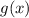
будет равно 
.
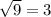Из той же формулы производной видно, что функция под корнем неограниченно возрастает при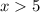
. Это значит, что функция 
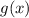не имеет максимального значения.
ответ: