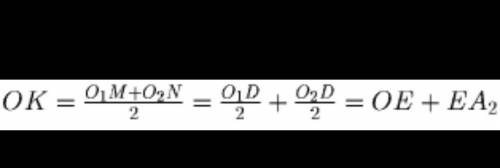.
Объяснение:
Обозначим центры окружностей, описанных около треугольников ADB и ADC через O1 и O2, а середины отрезков BD, DC, MN, DO2 и O1O2 — через A1, A2, K, E и O соответственно (см. рис.). Пусть ∠ BAD = ∠ CAD = α . Тогда ∠ A1O1D = ∠ A2O2D = α (так как половина центрального угла равна вписанному, опирающемуся на ту же дугу). Отрезок OK — средняя линия трапеции (или прямоугольника) O1MNO2, следовательно, OK ⊥ l, и (фото сверху). Заметим, что точки E, O и A2 лежат на одной прямой, так как ∠ OEO2 + ∠ O2EA2 = ∠ O1DO2 + ∠ O2EA2 = ∠ O1AO2 + (180° – ∠ DO2C) = 2 α + (180° – 2 α ) = 180°, т.е. OK = OE + EA2 = OA2. Аналогично доказывается, что OA1 = OK. Значит, точки A1, A2 и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.