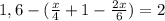
заменим десятичную дробь на обыкновенную, раскроем скобки, сократим дробь 2x/6 на два:
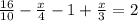
слагаемые с неизвестным оставим в левой части уравнения, поменяв их местами, числа перенесём в правую часть (при этом меняем их знак на противоположный), сократим дробь 16/10 на два:
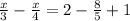
найдём Наименьший Общий Знаменатель всех трёх дробей (в данном случае это будет просто произведение всех знаменателей: 3*4*5 = 60); чтобы избавиться от дробей, домножим обе части уравнения на этот НОЗ:
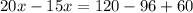
приведём подобные слагаемые в обеих частях уравнения (складываем и вычитаем):
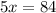
найдём икс, и представим ответ в виде десятичной дроби (домножив 84/5 на два):
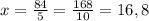
1) (2 корень 3 - 1)+ 2 корень 12=2 корень 3 - 1+4 корень 3=6 корень 3 - 1
2)(3х2-12)/(3х-7х+2)=3(х-2)(х+2)/(-4х+2)= -1,5(х-2)(х+2)/(2х-1) - не сокращается! Верно ли написано задание?
3) 3-(4х+1)(3-х)=х2, 3-(12х-4х2+3-х)=х2, 3-12х+4х2-3+х=х2, 4х2-11х=х2, 4х2-х2=11х, 3х2-11х=0, х*(3х-11)=0, х1=0, 3х-11=0, 3х=11, х2=11/3=3 целых 2/3.
4) средняя линия трапеции - отрезок, соединяющий середины боковых сторон этой трапеции. Она параллельна основаниям, равна их полусумме.
Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, РВСМ=РМDР - накрестлежащие, РВМС=РDМР - вертикальные), поэтому ВМ=МР или точка М - середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР: КМ = 1/2АР=1/2(АD+DF)=1/2(AD+BC)
преобразуем знаменатель, сгруппируем a*(a+b)-3*(a+b)=(a+b)(a-3)
теперь общая дробь: сократится множитель (a+b). остается ab*(a-b) / a-3