Если выкладываем 1 ряд то на первую клетку уйдет 4 палочки и 3 на каждую следующую
Каждый следующий ряд на первую клетку 3 палочки и по 2 на каждую следующую
Вариантов получить прямоугольник таким достаточно много
У Меня получились 402Х2, 286Х3, 86Х11, 79Х12, 56Х17 - можно дальше считать, мне кажется, что в условии не все данные
Для вычисления размеров надо по первому столбцу составить ряд 4,7,10,13,16 и т д
По второму 3,5,7,9,11 соответственно
Вычитаем из 2012 число из первого ряда и остаток делим на число из второго - должно делиться без остатка
А дальше посчитать периметр и учетверенную площадь легко
402Х2
P=804+4=808
S*4=804*4=3216
286X3
P=578
S*4=3432 и т.д.
я подозреваю что тут закралась неясность, в прогрессии насколько я помню количество элементов бесконечно, хотя в убывающей геометрической прогресии сумма всех элементов может сходиться.
инфми словами условие следует понимать так что n первых членов прогресии, где n = 2k,
выполняется условие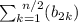 
в три раза больше, чем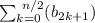 
рассмотрим это более подробно на примере первых шести элементов
сумма нечетных S(1,3,5) = b1 + b3 + b5
сумма четных S(2,4,6) = b2 + b4 + b6 = b1*q + b3*q + b5*q = q(b1 + b3 + b5) = q*S(1,3,5)
следовательно отношение между четной суммой и нечетной равно знаменателю прогрессии.
Для нашей задачи это число 3
ответ 3
Посмотреть в учебнике или поискать в интернете формулы для среднего арифметического и дисперсии. Только надо искать в разделе математической статистики, а не теории вероятности.
Что сделать - надо посмотреть, что можно вынести за скобку или за знак суммы.
Например - в сумме для среднего каждое число по условию увеличили на 3 и умножили на 2.
Значит каждое Xi стало 2*(Xi+3)
Задача состоит в том, чтобы сумму таких чисел выразить через сумму самих этих чисел:
Σ 2*(Xi+3) = 2*(X1+3) + 2*(X2+3) + .+2*(Xn+3) = 2*(X1+X2+...+Xn) + 2*3*n = 2*ΣXi + 6*n
Провести это рассуждение для формулы для среднего - и можно выразить Мновое через Мстарое. А Мстарое известно - 8.
Аналогично надо сообразить как преобразуется формула для дисперсии.
В конечном итоге, конечно, можно просто знать как влияют на среднее и на дисперсию общие аддитивные и мультипликативные члены. Ну так вывести эту закономерноть - лучший выучить.