х∈ (-2,5, 3).
Объяснение:
Решить систему неравенств:
-x > -3
2x+5>0
Первое неравенство:
-x > -3
х<3, знак меняется.
х∈(-∞, 3), интервал решений первого неравенства, при х от - бесконечности до 3.
Второе неравенство:
2x+5>0
2х> -5
x> -2,5
х∈(-2,5, +∞), интервал решений второго неравенства, при х от -2,5 до + бесконечности.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -2,5, 3.
Штриховка по первому неравенству от 3 до - бесконечности влево.
По второму неравенству штриховка от -2,5 вправо до + бесконечности.
Пересечение х∈ (-2,5, 3), это и есть решение системы неравенств.
Решите систему:
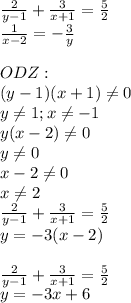
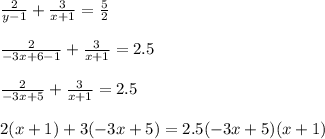
ODZ:
(x+1)(-3x+5)≠0
x≠-1 ; 1 2/3

x₁=(8+2)/10=1;
x₂=(8-2)/10=6/10=3/5
Подставим:
x₁=1
x₂=3/5 = 0.6
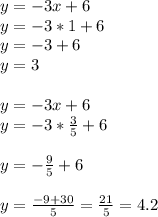
⇒⇒⇒⇒⇒⇒⇒⇒⇒⇒
y₁=3
y₂=4.2
Получим ответ:
(1;3) (0.6;4.2)
Вторая система:
3x²-2y²=1 ⇒ 3x²-2y²=1
2x²-y²=1 -4x²+2y²=-2
3x²-2y²-4x²+2y²=1+(-2)
-x²=-1
x²=1
x=±1
x₁=1
x₂=-1
Подставим:
2x²-y²=1
2-y²=1
-y²=-1
y²=1
y=±1
2x²-y²=1
2-y²=1
-y²=-1
y²=1
y=±1
Получим 4 решения:
(1;1) (-1;1) (1;-1) (-1;-1)
Третья система:
3x+y+2xy=-6 ⇒ 3x+y+2xy=-6
x+y+xy=-6 -2x-2y-2xy=12
3x+y+2xy-2x-2y-2xy=-6+12
x-y=6
-x+y=-6
y=-6+x
Подставим:
x+y+xy=-6
x+(-6+x)+x(-6+x)=-6
x-6+x-6x+x²+6=0
x²-4x=0
x(x-4)=0
x=0 или x-4=0
x=4
x₁=0
x₂=4
Подставим:
y=-6+x y=-6+x
y=-6+0 y=-6+4
y=-6 y=-2
y₁=-6
y₂=-2
Запишем решение;
(0;-6) (4;-2)
Велосипедист должен был проехать весь путь за 2 часа, т.е. расстояние составляет 2х км.
Известно, что велосипедист на весь путь затратил 1 и две третьих часа (или 5/3 часа.
Составим уравнение:
2х=5/3(х+3)
2х=5/3х+5
2х-5/3х=5
1/3х=5
х=5:1/3
х=15(км/ч)-планируемая скорость
Путь равен 2*15=30 (км)
ответ: 30 км.