А)4х-7(все это в корне)=3 б)х(в квадрате)-10х+1(все это в корне)=5 в)х(в квадрате)-3х(все это в корне)=2х-4(все - id272364720210414 от АндрееваДаша 14.04.2021 06:27

Question

Алгебра: А)4х-7(все это в корне)=3 б)х(в квадрате)-10х+1(все это в корне)=5 в)х(в квадрате)-3х(все это в корне)=2х-4(все это в корне) г)х(в квадрате)-3х(все это в корне)=х+3 ,

АндрееваДаша · Accepted Answer

Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.

Сумма второго и восьмого членов: 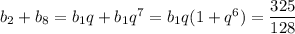$b_2+b_8=b_1q+b_1q^7=b_1q(1+q^6)=\dfrac{325}{128}$

Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:

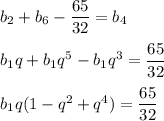
$b_2+b_6-\dfrac{65}{32}=b_4\\ \\ b_1q+b_1q^5-b_1q^3=\dfrac{65}{32}\\ \\ b_1q(1-q^2+q^4)=\dfrac{65}{32}$

Из равенства 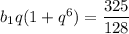$b_1q(1+q^6)=\dfrac{325}{128}$ заметим, что второй множитель можно разложить на множители по формуле суммы кубов

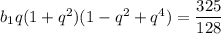
$b_1q(1+q^2)(1-q^2+q^4)=\dfrac{325}{128}$

Подставляем данные, получим

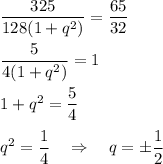
$\dfrac{325}{128(1+q^2)}=\dfrac{65}{32}\\ \\ \dfrac{5}{4(1+q^2)}=1\\ \\ 1+q^2=\dfrac{5}{4}\\ \\ q^2=\dfrac{1}{4}~~~\Rightarrow~~~ q=\pm \dfrac{1}{2}$

$b_1=\pm5$

ответ: 5; 0.5 и -5; -0.5.

А)4х-7(все это в корне)=3 б)х(в квадрате)-10х+1(все это в корне)=5 в)х(в квадрате)-3х(все это в корне)=2х-4(все это в корне) г)х(в квадрате)-3х(все это в корне)=х+3 ,

MOGZ ответил