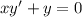
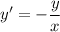 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными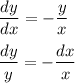
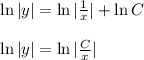
 - общее решение
- общее решение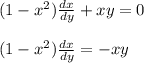

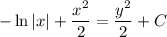 - общий интеграл
- общий интеграл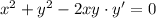

 , тогда
, тогда 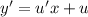



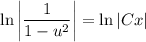
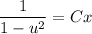
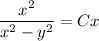 - общий интеграл
- общий интеграл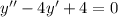
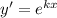 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
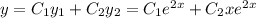 - общее решение
- общее решение
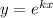 , тогда получаем
, тогда получаем
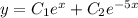

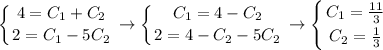
 - частное решение
- частное решение
35056485
Числа x₁ и x₂ корни уравнения x²- (2a-3)x+a²-3=0. При каких значениях параметра a выполняются равенство 2(x₁ + x₂) = x₁* x₂
* * * 2(x1 + x2) = x1,x2? * * *
решение: x² - (2a - 3)x + a² - 3 = 0
D =(2a - 3)² -4(a² - 3) = 4a² - 12a + 9 - 4a² +12 =21 -12a =3(7 -4a)
Уравнение имеет решение , если D ≥ 0 ⇔ 3(7 -4a) ≥ 0
⇒ 7 - 4a ≥ 0 ⇔ a ≤ 7/4 a ∈ ( -∞ ; 1 ,75 ]
- - - - - - -
2(x₁ + x₂) = x₁* x₂ по теореме BИЕТА
2(2a-3) = a²- 3 ⇔ a² - 4a+3 =0 ⇒ a₁ = 1 , a₂ =3_посторонний корень.
При a = 3 квадратное уравнение не имеет решения
1 ∈ ( -∞ ; 1 ,75 ] , но 3 ∉ ( -∞ ; 1 ,75 ]
* * * при a = 3 : x²- 3x + 6 =0 D =3² -4*6 = -15 < 0 * * *
ответ : 1 .
* * * a² - 4a+3 =a² - a - 3a +3 =a(a-1) - 3(a-1) =(a-1)(a-3)
* * * a² - 4a+3 =(a - 2)² - 1 = (a - 2 + 1) (a-2 -1) = (a - 1) (a-3)
* * * a₁ ,₂ = 2 ± √(4 -3) = 2 ±1
чтобы число делилось на 5 нужно чтобы оно оканчивалось на 0 или 5. если наше число будет оканчиваться на 0, то и первая цифра должна будет равна 0, но тогда число станет 4-значным, т.е число оканчивается на 5, значит и 1-я цифра будет 5
5усу5.
т.к. мы ищем наименьшее число, то нужно подставить на места неизвестных цифр наименьшие, а таковым является 0.
т.е. получим число 50005
2) 12+15=27 - всего детей играет во дворе
3+4=7 - играют в вышибалу
27-7=20 - всего играют в футбол
12-3=9 - девочек играют в футбол
9/20=0,45 - вероятность того, что портфель принадлежит девочке, играющей в футбол