В решении.
Объяснение:
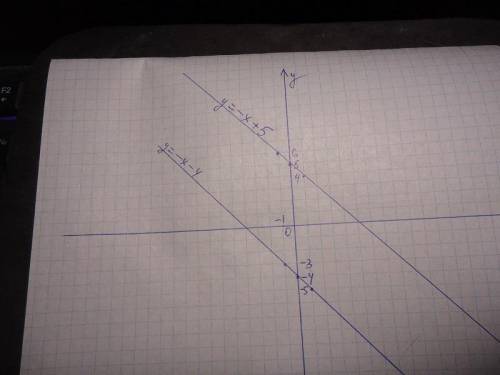
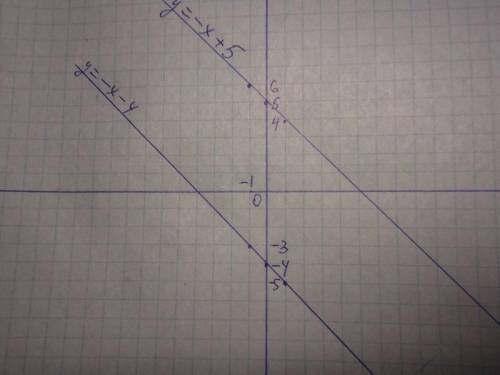
Построить графики функций у= -х-4, у= -х+5, у=-х в той же системе координат.
Сделать вывод: что происходит, если k одинаковое, но меняется b в формуле.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у = -х - 4 у = -х + 5
Таблицы:
х -1 0 1 х -1 0 1
у -3 -4 -5 у 6 5 4
Согласно графика, вывод: если k равны, а b разные, графики уравнений параллельны.
Объяснение:
a) у²-6у+5=0;
a=1; b=-6; c=5.
D=b²-4ac= (-6)²-4*1*5=36-20=16>0 два корня.
у1=5; у2=1.
у²-6у+5=(y-5)(y-1).
***
б) x²+14x+24=0;
a=1; b=14; c=24;
D=b²-4ac=14²-4*1*24=196-96=100>0 - два корня.
x1=-12; x2=-2.
x²+14x+24=(x+12)(x+2).
***
в) −y²+14y=33; [*(-1)]
y²-14y+33=0;
a=1; b=-14; c=33;
D=b²-4ac=(-14)²-4*1*33=196- 132= 64>0 - два корня;
y1=11; y2=3;
y²-14y+33=(y-11)(y-3).
***
г) −x²−10x−16=0; [*(-1)]
x²+10x+16=0;
a=1; b=10; c=16;
D=b²-4ac=10²-4*1*16=100-64=36>0 - два корня;
x1=-8; x2=-2;
x²+10x+16=(x+8)(x+2).
***
д) x²−8x−48=0;
a=1; b=-8; c=-48;
D=b²-4ac=(-8)²-4*1*(-48)=64+192=256;
x1=12; x2= -4;
x²−8x−48=(x-12)(x+4).
***
е) y²+16y+55=0;
a=1; b=16; c=55;
D=b²-4ac=16²-4*1*55= 256- 220=36>0 - два корня;
y1=-11; y2=-5;
y²+16y+55=(y+11)(y+5).
***
ж) x²−24x+144=0;
a=1; b=-24; c=144;
D=b²-4ac=(-24)²-4*1*144= 576 -576=0 - два равных корня.
x1=x2=12;
x²−24x+144=(x-12)(x-12)=(x-12)².
***
з) −y2+18y−81=0; [*(-1)]
y²-18y+81=0;
a=1; b=-18; c= 81;
D=b²-4ac=(-18)²-4*1*81=324-324=0 - два равных корня;
y1=9; y2=9.
y²-18y+81=(y-9)(y-9)=(y-9)².
Как-то странно получилось...