ответ:
объяснение:
берем переменные арифметич. прогрессии a b c. по формуле сумма 3 первых членов равна:
((а+с) /2)*3=15, отсюда a+c=10 отсюда с=10-a
также исходя, что у нас арифметика. прогрессия: c=a+2*t, где t - шаг прогрессии. из посл двух уравнений приравниваем: 10-a=a+2*t, отсюда t=5-a.
также 2-й член арифметика. прогрессии: b=a+t=a+(5-a)=5.
пусть первые члены прогрессии будут x y z. тогда х=a+1, y=b+3=8, z=c+9.
если сложить x и z получим: x+z=a+1+c+9=(a+c)+10, а из 1-го уравнения a+c=10, получаем x+z=10+10=20, отсюда х=20-z.
знаменатель процессии равен: z/y=y/x, отсюда z/8=8/(20-z), отсюда квадратное уравнение z2-20z+64=0, находим z=16, отсюда c=7, a=10-7=3.
получаем х=4, y=8, z=16. знаменатель прогрессии равен 2. следующие 3 члена . прогрессии: 32, 64, 128. сумма: 252.
Двузначное число, где а десятков и b единиц представим в виде 10a+b (это разложение числа по разрядам). Далее записываем условие задачи: 1) первое предложение
(10a+b):(a+b)=7(ост.3)
10a+b=7(a+b)+3
10a+b=7a+7b+3
3a-6b=3
a-2b=1 - это первое уравнение системы.
2) читаем второе предложение задачи
При перестановке цифр данного двузначного числа получим число 10b+a. Известно, что оно на 36 меньше, чем число 10a+b. Запишем это: 10a+b-36=10b+a
9a-9b=36 |:9
a-b=4 - это второе уравнение системы
Решаем систему:
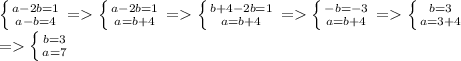
Итак, искомое двузначное число равно 73.
x=1 x=-1
+ _ +
-1 1
max min
ymax=-1+3+2=4 (-1;4)