ответ: 2^97
Объяснение:
Найдем наибольшую степень двойки что меньше чем 100.
Очевидно что это 2^6=64 (2^7=128>100)
Понятно ,что число содержащее 6 двоек единственно n1=1 .
Теперь разберемся как посчитать число чисел которые кратны только на 2^5 ( не больше чем на эту степень двоек)
Все числа кратные на 2^5 можно записать так:
2^5 ,2^5*2 ;2^5*3 ;2^5*42^5*n . Соответственно из всех n нас интересуют только нечетные , при этих n число будет кратно ровно на 2^5.
Найдем максимальное n, что 32*n<100
Очевидно что nmax=3 (3*32=96) (число нечетных чисел тут равно n2=2)
Для справки сразу скажем ,что число нечетных чисел на интервале от 1 до k равно k/2- если k-четное и (k+1)/2 ,если k-нечетное.
По аналогии посчитаем число таких чисел для 2^4=16
nmax=6 (6*16=96) (число нечетных чисел n3=6/2=3)
Для 2^3=8 :
nmax=12 (8*12=96) (n4=12/2=6)
Для 2^2=4 :
nmax=25 (4*25=100) ( n5=(25+1)/2=13)
Для 2^1=2
nmax=50 (2*50=100) (n6=50/2=25)
Осталось посчитать общее количество двоек:
N=6n1+5n2+4n3+3n4+2n5+n6=6+10+12+18+26+25=97
Значит 100! делится на 2^97.
Парабола – график квадратичной функции. Этот график позволяет прослеживать основные свойства функции в зависимости от вида квадратичной функции.
Существуют различные преобразования графиков, если тебе нужно узнать поподробнее об этом напиши в комментариях и я объясню.
Мы рассмотрим только все самое основное.
В функции y= a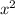
От коэффициента а зависит то куда направлены ветви параболы и то, как они идут.
Если коэффициент а>0, тогда ветви будут идти вверх.
Если коэффициент а<0, тогда ветви будут идти вниз.
От этого коэффициента и зависит то, как они выглядят.
Если коэффициент больше 1, то парабола будет идти резче вверх, а то, насколько он больше 1 будет показателем того насколько она идет резче по оси оу.
Если коэффициент больше 0, но меньше 1, то парабола будет более прижатой к оси абсцисс (ох), а коэффициент будет показателем того насколько она прижата к оси.
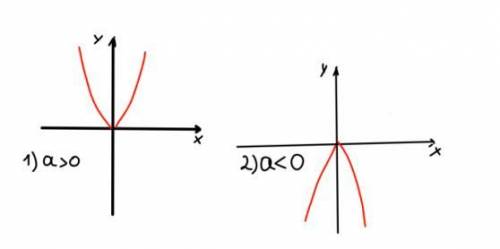
Для этого на примере рассмотрим графики функций у=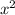 , у=2
, у=2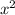 и у=
и у=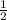
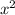
Заранее прощения не за самые ровные графики.
На этом графике мы видим подтверждение ранее сказанного правила.
По функции можно сразу определять каким будет график параболы.
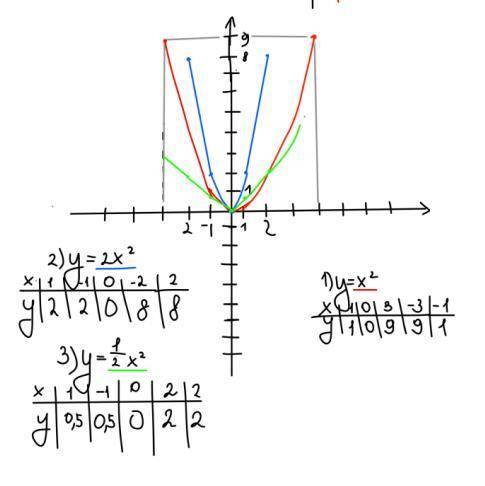
3-3x≥2
3x≤1
x≤1/3
б) -x^2+3x-2<0
x²-3x+2>0
(x-1)(x-2)>0
12
x=(-oo 1)U (2+oo)
в) x-4/2<3 + x-1/5
5x-20<30+2x-2
3x<48
x<16