y=kx+m
График проходит через начало координаn, следовательно m=0
Найдем уравнение прямой, проходящей через точки N(4;1) и M(-3;-1) при системы :
\left \{ {{1=4k+m} \atop {-1=-3k+m}} \right.
\left \{ {{m=1-4k} \atop {-1=-3k+m}} \right.
\left \{ {{m=1-4k} \atop {-1=-3k+1-4k}} \right.
-1=-3k+1-4k
7k=2
k=2/7
\left \{ {{m=1-4k} \atop {k=2/7}} \right.
\left \{ {{m=-1/7} \atop {k=2/7}} \right.
y=(2/7)x+(-1/7)
условие паралельности : k1=k1, m1 \neq m2
Итак, мы можем составить множество прямых, параллельной данной, с условием того, что k=2/7, m1 \neq -1/7 всегда
Одной из таких прямых является прямая
y=(2/7)x
жуть
вообщем в уравнении y=kx+m
k всегда равен 2/7
m никогда не равен -1/7
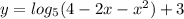
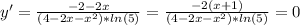
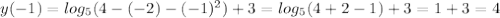
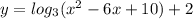
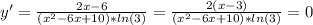
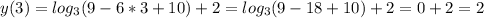
x=2/5
x=0,4
б)9-4х=1
-4x=1-9
-4x=-8
x=2
в)3х-х+5х=2.1
7x=2.1
x=2.2/7
x=0,3
г)2(у+2)=-3(у-1)
2y+4=-3y+3
2y+3y=3-4
5y=-1
y=-0,2
е)3у-11=1-2у
3y+2y=11+1
5y=12
y=12/5
y=2,4
ж)у+4=2у-5
y-2y=-5-4
-y=-9
y=9
3)7(у-3)=-2(у+3)
7y-21=-2y-6
7y+2y=21-6
9y=15
y=5/3
к)6х-10х+х=0.3
-3x=0,3
x=0,3/(-3)
x=-0,1
л)0.7х+0.8х-х=2
0,5x=2
x=2/0,5
x=4